Preliminary

Perceptron

• Threshold unit
  • “Fires” if the weighted sum of inputs exceeds a threshold
• Soft perceptron
  • Using sigmoid function instead of a threshold at the output
  • Activation: The function that acts on the weighted combination of inputs (and threshold)
• Affine combination
  • Different from Linear combination: the result of mapping zero is not zero.

Multi-layer perceptron

• Depth
  • Is the length of the longest path from a source to a sink
  • Deep: Depth greater than 2
• Inputs/Outputs are real or Boolean stimuli
• What can this network compute?

Universal Boolean functions

• A perceptron can model any simple binary Boolean gate
  • Using weight 1 or -1 to model function
  • The universal AND gate: $(\bigwedge_{i=1}^{L} X_{i}) \wedge(\bigwedge_{i=L+1}^{N} \bar{X}_{i})$
  • The universal OR gate: $(\bigvee_{i=1}^{L} X_{i}) \vee(\bigvee_{i=L+1}^{N} \bar{X}_{i})$
  • Cannot compute an XOR
• MLPs can compute the XOR

• MLPs are universal Boolean functions

  • Can compute any Boolean function

• A Boolean function is just a truth table

  • So expressed the result in disjunctive normal form, like

$\begin{aligned} Y=& \bar{X}_1 \bar{X}_2 X_3 X_4 \bar{X}_5+\bar{X}_1 X_2 \bar{X}_3 X_4 X_5+\bar{X}_1 X_2 X_3 \bar{X}_4 \bar{X}_5+X_1 \bar{X}_2 \bar{X}_3 \bar{X}_4 X_5+X_1 \bar{X}_2 X_3 X_4 X_5+X_1 X_2 \bar{X}_3 \bar{X}_4 X_5 \end{aligned}$

• In this case, need 5 neurons in the hidden layer.

Need for depth

• A one-hidden-layer MLP is a Universal Boolean Function

  • But the largest number of perceptrons is expontial: $2^N$

• How about depth?

  • Will require $3(N-1)$ perceptrons, linear in $N$ to express the same function
  • Using associatable rules, can be arranged in $2\log_2 N$ layers
  • eg. model $O=W \oplus X \oplus Y \oplus Z$

  

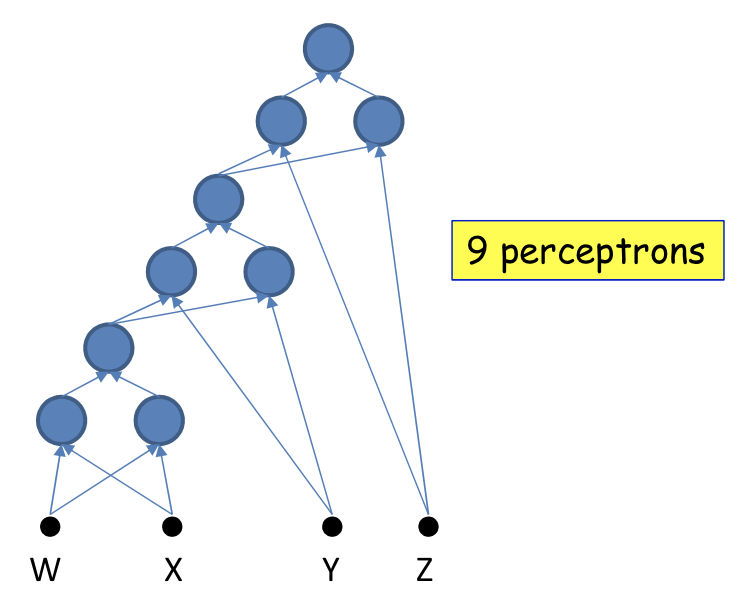
• The challenge of depth

  • Using only $K$ hidden layers will require $O(2^{CN})$ neurons in the $K$th layer, where $C = 2^{-(k-1)/2}$
  • A network with fewer than the minimum required number of neurons cannot model the function

Universal classifiers

• Composing complicated “decision” boundaries

• Using OR to create more decision boundaries
  • Can compose arbitrarily complex decision boundaries
  • Even using one-layer MLP

Need for depth

• A naïve one-hidden-layer neural network will required infinite hidden neurons
• Construct basic unit and add more layers to decrese #neurons
• The number of neurons required in a shallow network is potentially exponential in the dimensionality of the input

Universal approximators

• A one-layer MLP can model an arbitrary function of a single input
• MLPs can actually compose arbitrary functions in any number of dimensions
  • Even without "activation"
• Activation
  • A universal map from the entire domain of input values to the entire range of the output activation

Optimal depth and width

• Deeper networks will require far fewer neurons for the same approximation error
• Sufficiency of architecture
  • Not all architectures can represent any function
• Continuous activation functions result in graded output at the layer
  • To capture information "missed" by the lower layer

Width vs. Activations vs. Depth

• Narrow layers can still pass information to subsequent layers if the activation function is sufficiently graded
  • But will require greater depth, to permit later layers to capture patterns
• Capacity of the network
  • Information or Storage: how many patterns can it remember
  • VC dimension: bounded by the square of the number of ..weights.. in the network
  • Straight forward: largest number of disconnected convex regions it can represent
• A network with insufficient capacity cannot exactly model a function that requires a greater minimal number of convex hulls than the capacity of the network