a way to solve minimization problem

Problem setup

• Input-output pairs: not to mention

• Representing the output: one-hot vector

  • $y_{i}=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)}$

  • two classes of softmax = sigmoid

• Divergence: must be differentiable

  • For real-valued output vectors, the (scaled) $L_2$ divergence

    • $\operatorname{Div}(Y, d)=\frac{1}{2}\|Y-d\|^{2}=\frac{1}{2} \sum_{i}\left(y_{i}-d_{i}\right)^{2}$

  • For binary classifier

    • $\operatorname{Div}(Y, d)=-\operatorname{dlog} Y-(1-d) \log (1-Y)$

    • Note: the derivative is not zero even $d = Y$, but it can converge very quickly

  • For multi-class classification

    • $\operatorname{Div}(Y, d)=-\sum_{i} d_{i} \log y_{i}=-\log y_{c}$

    • If $y_c < 1$ , the slope is negative w.r.t. $y_c$, indicates increasing $y_c$ will reduce divergence

Train the network

Distributed Chain rule

$y=f\left(g_{1}(x), g_{1}(x), \ldots, g_{M}(x)\right)$

$\frac{d y}{d x}=\frac{\partial f}{\partial g_{1}(x)} \frac{d g_{1}(x)}{d x}+\frac{\partial f}{\partial g_{2}(x)} \frac{d g_{2}(x)}{d x}+\cdots+\frac{\partial f}{\partial g_{M}(x)} \frac{d g_{M}(x)}{d x}$

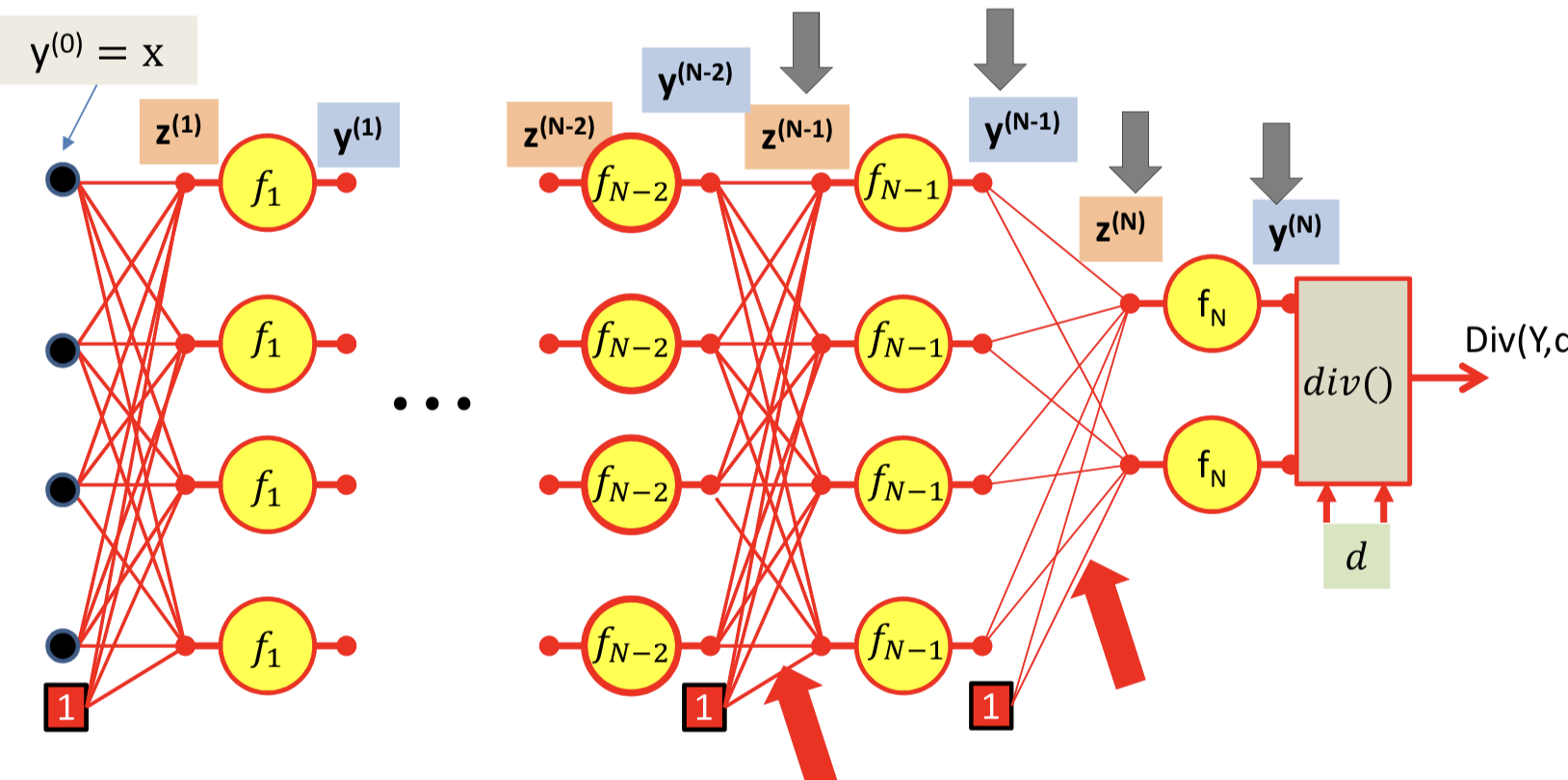
Backpropagation

• For each layer: we caculate $\frac{\partial D i v}{\partial y_{i}}$,$\frac{\partial Dicv}{\partial z}$, and $\frac{\partial Div}{\partial w_{ij}}$

• For ouput layer

  • It is easy to caculate $\frac{\partial D i v}{\partial y_{i}^{(N)}}$
  • So: $\frac{\partial D i v}{\partial z_{i}^{(N)}}=f_{N}^{\prime}\left(z_{i}^{(N)}\right) \frac{\partial D i v}{\partial y_{i}^{(N)}}$
  • $\frac{\partial D i v}{\partial w_{ij}^{(N)}}=\frac{\partial z_{j}^{(N)}}{\partial w_{ij}^{(N)}} \frac{\partial D i v}{\partial z_{j}^{(N)}}$, where $\frac{\partial z_{j}^{(N)}}{\partial w_{ij}^{(N)}} = y_i^{(N)}$

• Pass on

  • $z_{j}^{(N)}=\sum_{i} w_{i j}^{(2)} y_{i}^{(v-1)}$, so $\frac{\partial z_{j}^{(N)}}{\partial y_{1}^{(N-1)}} = w_{ij}^{(N)}$
  • $\frac{\partial D i v}{\partial y_{i}^{(N-1)}}=\sum_{j} w_{i j}^{(N)} \frac{\partial D i v}{\partial z_{j}^{(N)}}$
  • $\frac{\partial D i v}{\partial z_{i}^{(N-1)}}=f_{N-1}^{\prime}(z_{i}^{(N-1)}) \frac{\partial D i v}{\partial y_{i}^{(N-1)}}$
  • $\frac{\partial D i v}{\partial w_{i j}^{(N-1)}}=y_{i}^{(N-2)} \frac{\partial D i v}{\partial z_{j}^{(N-1)}}$

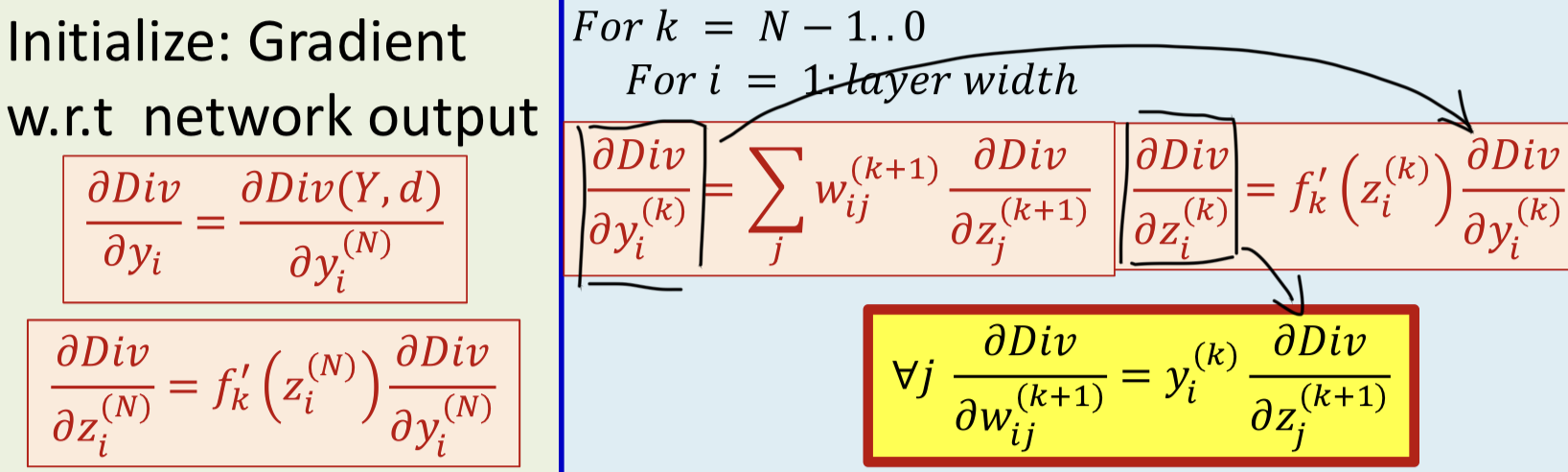
Special case

Vector activations

• Vector activations: all outputs are functions of all inputs

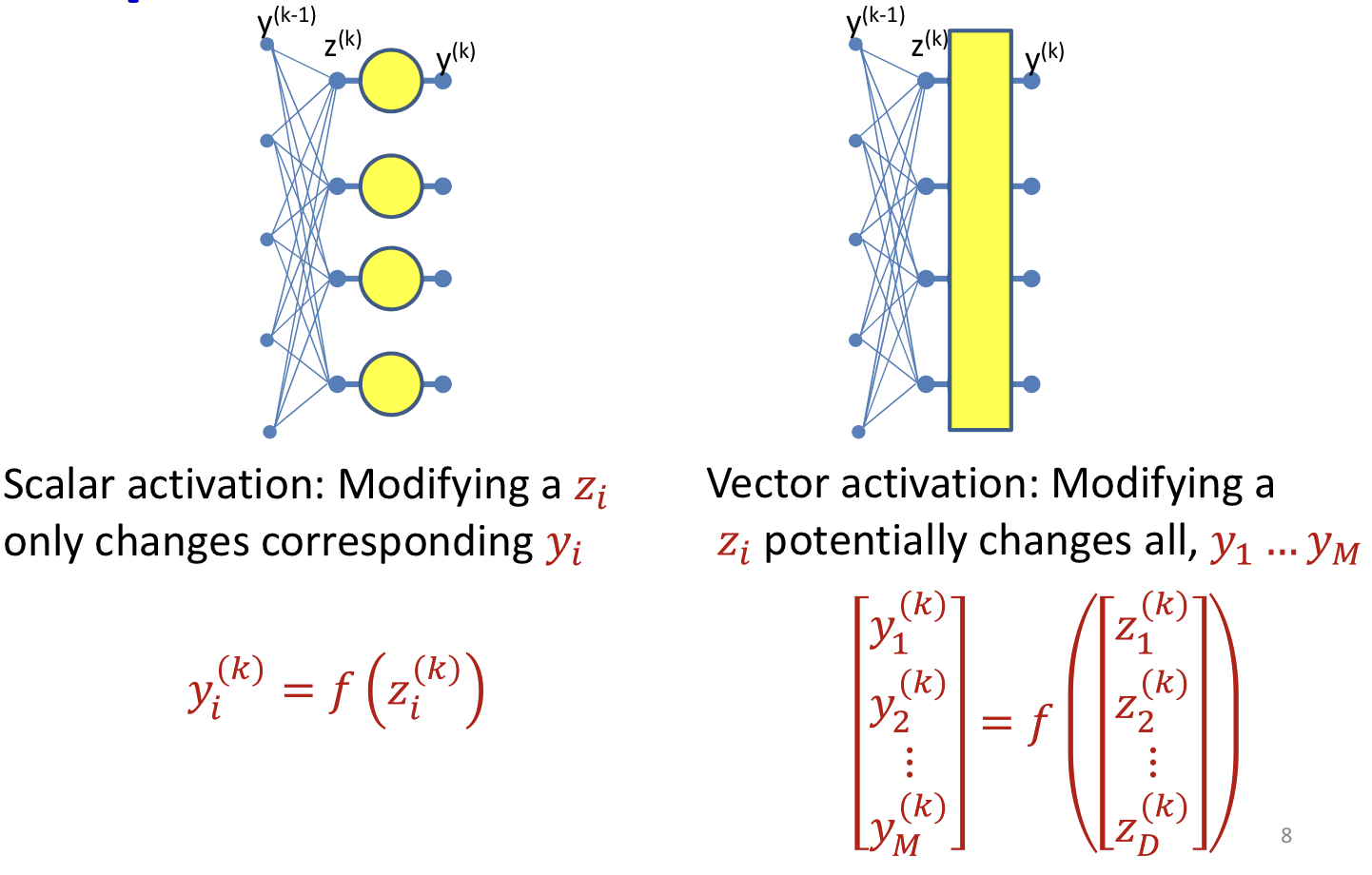
• So the derivatives need to change a little

• $\frac{\partial D i v}{\partial z_{i}^{(k)}}=\sum_{j} \frac{\partial D i v}{\partial y_{j}^{(k)}} \frac{\partial y_{j}^{(k)}}{\partial z_{i}^{(k)}}$

• Note: derivatives of scalar activations are just a special case of vector activations:

• $\frac{\partial y_{j}^{(k)}}{\partial z_{i}^{(k)}}=0 \text { for } i \neq j$

• For example, Softmax:

$y_{i}^{(k)}=\frac{\exp \left(z_{i}^{(k)}\right)}{\sum_{j} \exp \left(z_{j}^{(k)}\right)}$

$\frac{\partial D i v}{\partial z_{i}^{(k)}}=\sum_{j} \frac{\partial D i v}{\partial y_{j}^{(k)}} \frac{\partial y_{j}^{(k)}}{\partial z_{i}^{(k)}}$

$\frac{\partial y_{j}^{(k)}}{\partial z_{i}^{(k)}}=\left\{\begin{array}{c} y_{i}^{(k)}\left(1-y_{i}^{(k)}\right) \quad \text { if } i=j \\ -y_{i}^{(k)} y_{j}^{(k)} \quad \text { if } i \neq j \end{array}\right.$

• Using Keonecker delta $\delta_{i j}=1$ if $i=j, \quad 0$ if $i \neq j$

$\frac{\partial D i v}{\partial z_{i}^{(k)}}=\sum_{j} \frac{\partial D i v}{\partial y_{j}^{(k)}} y_{i}^{(k)}\left(\delta_{i j}-y_{j}^{(k)}\right)$

Multiplicative networks

• Some types of networks have multiplicative combination(instead of additive combination)
• Seen in networks such as LSTMs, GRUs, attention models, etc.

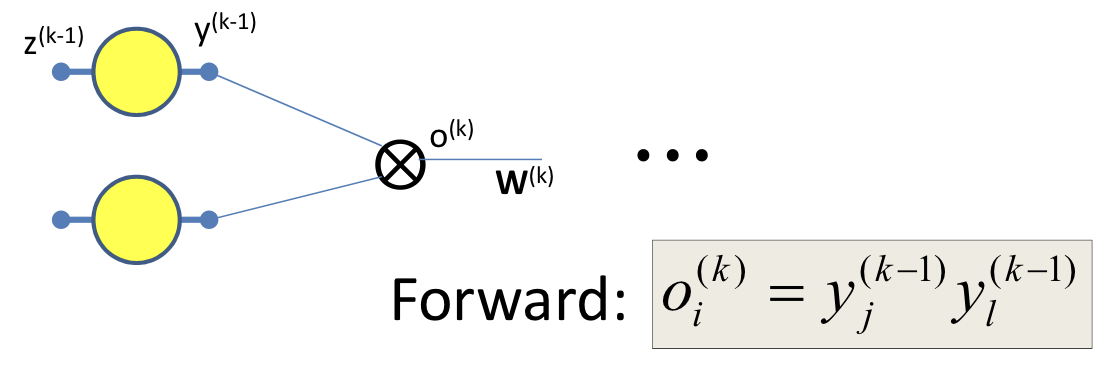
• So the derivatives need to change

$\frac{\partial D i v}{\partial o_{i}^{(k)}}=\sum_{j} w_{i j}^{(k+1)} \frac{\partial D i v}{\partial z_{j}^{(k+1)}}$

$\frac{\partial D i v}{\partial y_{j}^{(k-1)}}=\frac{\partial o_{i}^{(k)}}{\partial y_{j}^{(k-1)}} \frac{\partial D i v}{\partial o_{i}^{(k)}}=y_{l}^{(k-1)} \frac{\partial D i v}{\partial o_{i}^{(k)}}$

• A layer of multiplicative combination is a special case of vector activation

Non-differentiable activations

• Activation functions are sometimes not actually differentiable

  • The RELU (Rectified Linear Unit)
    • And its variants: leaky RELU, randomized leaky RELU
  • The “max” function

• Subgradient

  • $\left(f(x)-f\left(x_{0}\right)\right) \geq v^{T}\left(x-x_{0}\right)$

    • The subgradient is a direction in which the function is guaranteed to increase

    • If the function is differentiable at $x$ , the subgradient is the gradient

    • But gradient is not always the subgradient though

Vector formulation

• Define the vectors:

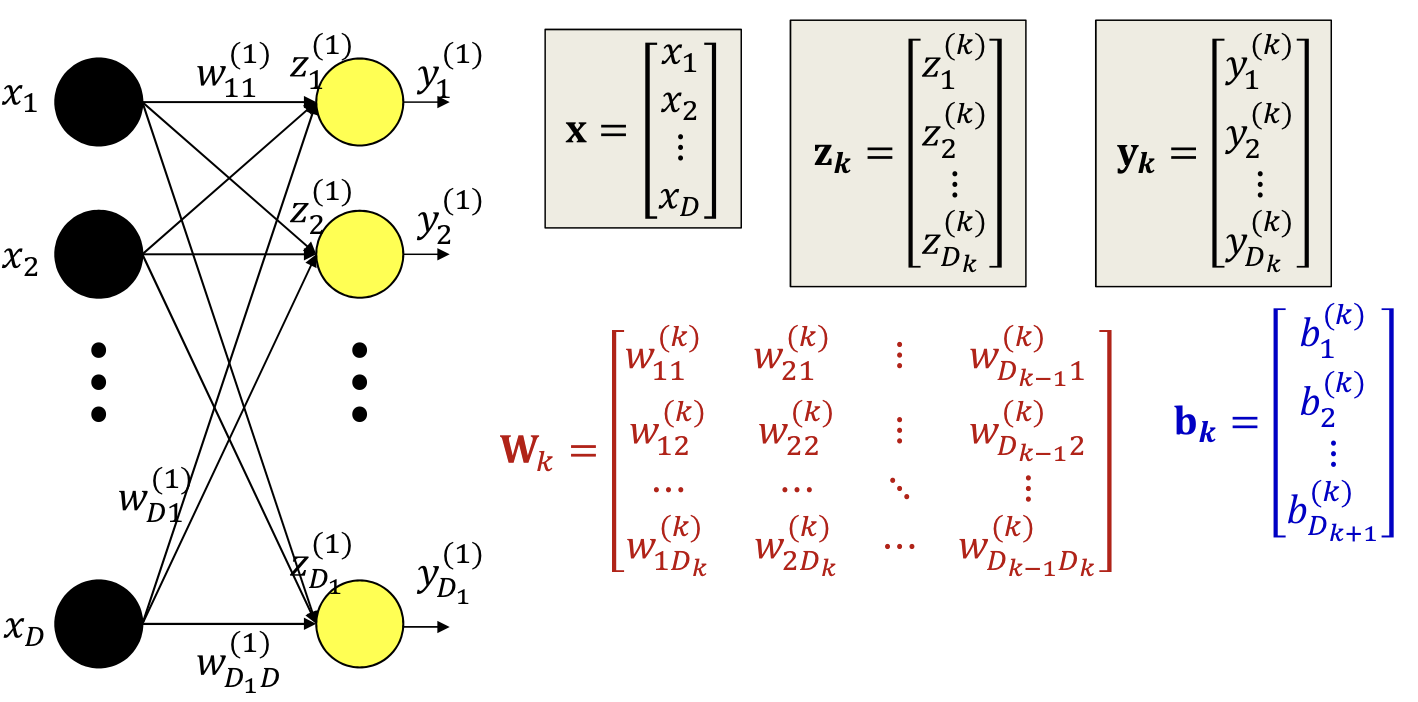
Forward pass

Backward pass

• Chain rule
  • $\mathbf{y}=\boldsymbol{f}(\boldsymbol{g}(\mathbf{x}))$
  • Let $z = g(x)$,$y = f(z)$
  • So $J_{\mathbf{y}}(\mathbf{x})=J_{\mathbf{y}}(\mathbf{z}) J_{\mathbf{z}}(\mathbf{x})$
• For scalar functions:
  • $D = f(Wy + b)$
  • Let $z = Wy + b$, $D = f(z)$
  • $\nabla_{x} D = \nabla_z(D)J_z(x)$
• So for backward process
  • $\nabla_{Z_N} Div = \nabla_Y Div \nabla_{Z_N}Y$
  • $\nabla_{y_{N-1}}Div = \nabla_{Z_N} Div \nabla_{y_{N-1}} z_N$
  • $\nabla_{W_N} Div = y_{N-1} \nabla_{Z_N} Div$
  • $\nabla_{b_N} Div = \nabla_{Z_N} Div$
• For each layer
  • First compute $\nabla_{y} Div$
  • Then compute $\nabla_{z}Div$
  • Finally $\nabla_{W} Div$, $\nabla_{b} Div$

Training

Analogy to forward pass