Stability

• Will this necessarily be「Bounded Input Bounded Output」?
  • Guaranteed if output and hidden activations are bounded
  • But will it saturate？

Analyzing Recursion

• Sufficient to analyze the behavior of the hidden layer since it carries the relevant information

• Assumed linear systems

  • $z_{k}=W_{h} h_{k-1}+W_{x} x_{k}, \quad h_{k}=z_{k}$

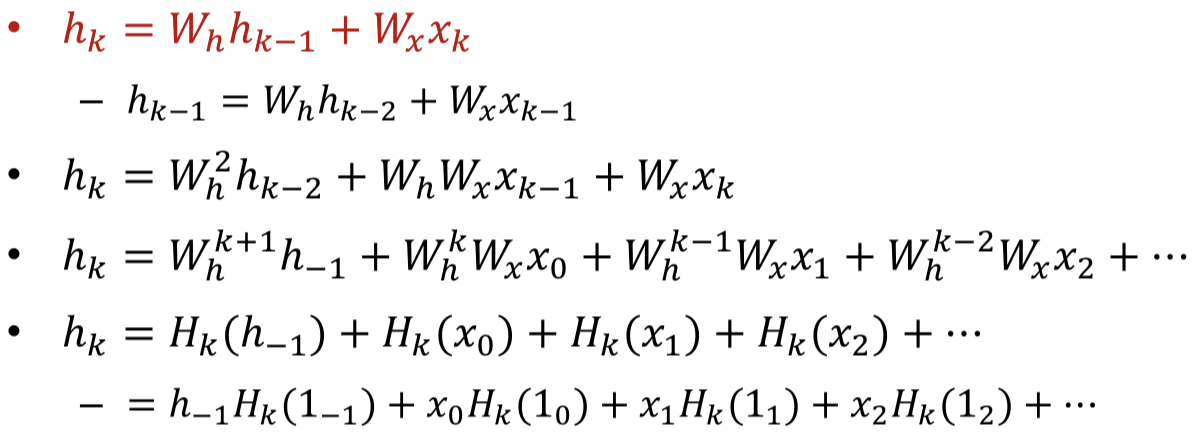
• Sufficient to analyze the response to a single input at $t =0$ (else is zero input)

Simple scalar linear recursion

• $h(t) = wh(t-1) + cx(t)$
• $h_0(t) = w^tcx(0)$
• If $w > 1$ it will blow up

Simple Vector linear recursion

• $h(t) = Wh(t-1) + Cx(t)$
• $h_0(t) = W^tCx(0)$
• 
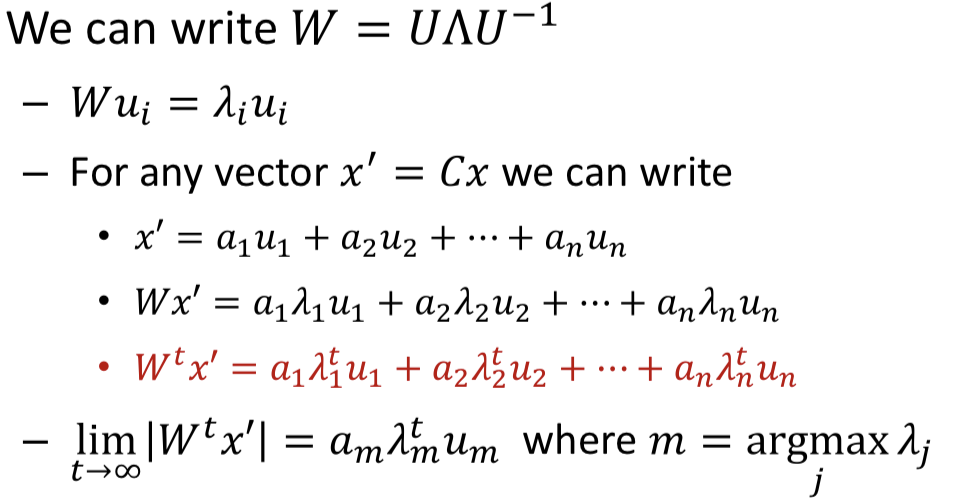
• For any input, for large the length of the hidden vector will expand or contract according to the $t-$ th power of the largest eigen value of the hidden-layer weight matrix
• If $|\lambda_{max} > 1|$ it will blow up, otherwise it will contract and shrink to 0 rapidly

Non-linearities

• Sigmoid: Saturates in a limited number of steps, regardless of $w$
  • To a value dependent only on $w$ (and bias, if any)
  • Rate of saturation depends on $w$
• Tanh: Sensitive to $w$, but eventually saturates
  • “Prefers” weights close to 1.0
• Relu: Sensitive to $w$, can blow up

Lessons

• Recurrent networks retain information from the infinite past in principle
• In practice, they tend to blow up or forget
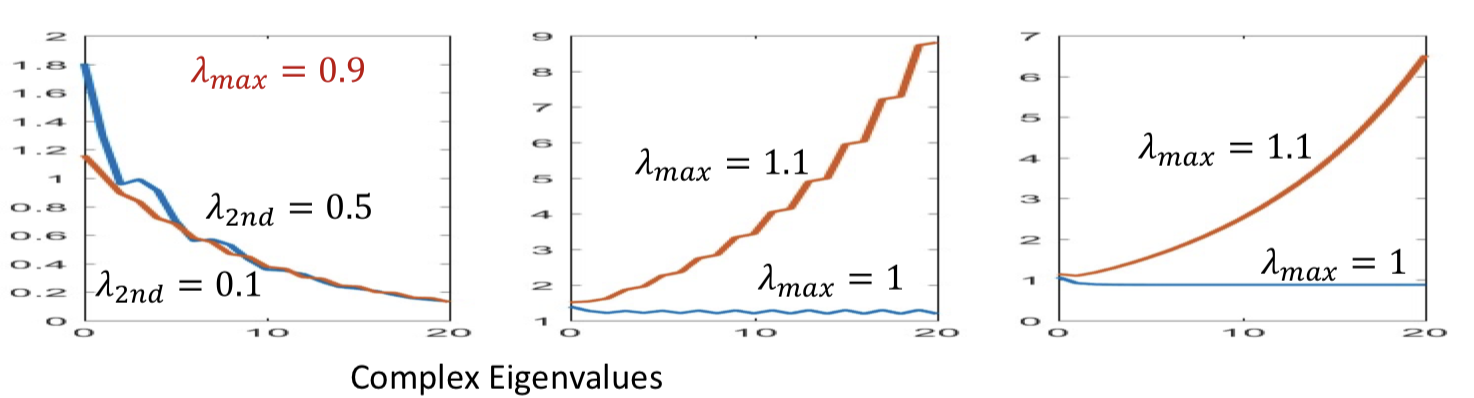
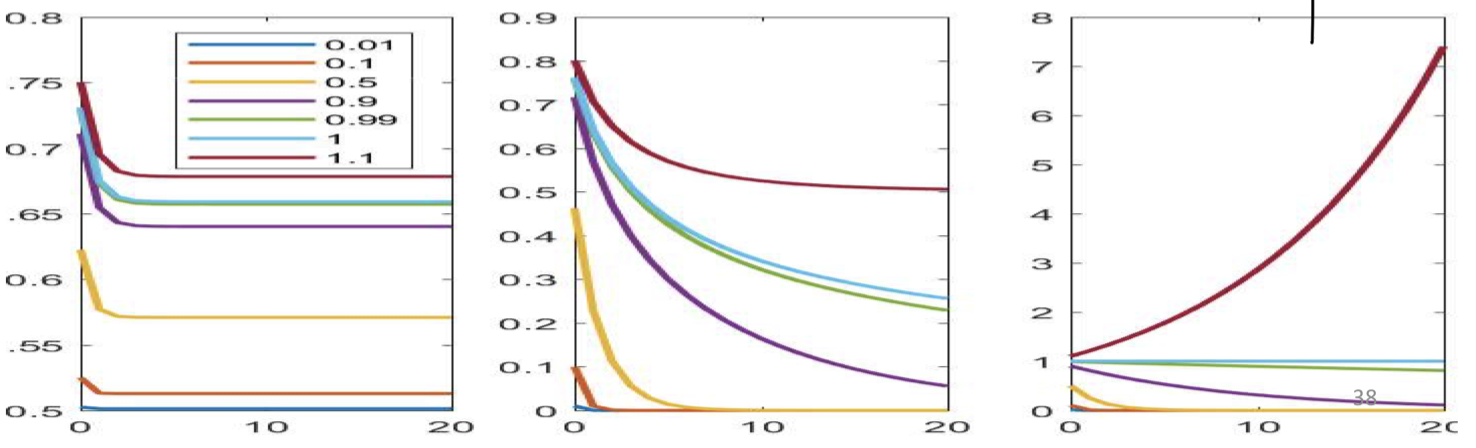
  • If the largest Eigen value of the recurrent weights matrix is greater than 1, the network response may blow up
  • If it’s less than one, the response dies down very quickly
• The “memory” of the network also depends on the parameters (and activation) of the hidden units
  • Sigmoid activations saturate and the network becomes unable to retain new information
  • RELU activations blow up or vanish rapidly
  • Tanh activations are the most effective at storing memory
    • And still has very short “memory”
    • Still sensitive to Eigenvalues of $W$

Vanishing gradient

• A particular problem with training deep networks is the gradient of the error with respect to weights is unstable
• For
  • $\operatorname{Div}(X)=D\left(f_{N}\left(W_{N-1} f_{N-1}\left(W_{N-2} f_{N-2}\left(\ldots W_{0} X\right)\right)\right)\right)$
• We get
  • $\nabla_{f_{k}} \operatorname{Div}=\nabla D . \nabla f_{N} . W_{N-1} . \nabla f_{N-1} . W_{N-2} \ldots \nabla f_{k+1} W_{k}$
• Where
  • $\nabla{f_{n}}$ is jacobian of $f_N()$ to its current input

For activation

• For RNN
  • $\nabla f_{t}\left(z_{i}\right)=\left[\begin{array}{cccc}f_{t, 1}^{\prime}\left(z_{1}\right) & 0 & \cdots & 0 \\\\ 0 & f_{t, 2}^{\prime}\left(z_{2}\right) & \cdots & 0 \\\\ \vdots & \vdots & \ddots & \vdots \\\\ 0 & 0 & \cdots & f_{t, N}^{\prime}\left(z_{N}\right)\end{array}\right]$
  • For vector activations: A full matrix
  • For scalar activations: A matrix where the diagonal entries are the derivatives of the activation of the recurrent hidden layer
• The derivative (or subgradient) of the activation function is always bounded
• Most common activation functions, such as sigmoid, tanh() and RELU have derivatives that are always less than 1
  • Multiplication by the Jacobian is always a shrinking operation
  • After a few layers the derivative of the divergence at any time is totally “forgotten”

For weights

• In a single-layer RNN, the weight matrices are identical
  • The conclusion below holds for any deep network, though
• The chain product for $\nabla_{f_k} Div$ will
  • Expand $\nabla D$ along directions in which the singular values of the weight matrices are greater than 1
  • Shrink $\nabla D$ in directions where the singular values are less than 1
  • Repeated multiplication by the weights matrix will result in Exploding or vanishing gradients

LSTM

Problem

• Recurrent nets are very deep nets
• Stuff gets forgotten in the forward pass too
  • Each weights matrix and activation can shrink components of the input
• Need the long-term dependency
• The memory retention of the network depends on the behavior of the weights and jacobian
• Which in turn depends on the parameters $W$ rather than what it is trying to remember
• We need
  • Not be directly dependent on vagaries of network parameters, but rather on input-based determination of whether it must be remembered
  • Retain memories until a switch based on the input flags them as ok to forget
    • 「Curly brace must remember until curly brace is closed」
• LSTM
  • Address the problem of input-dependent memory behavior

Architecture

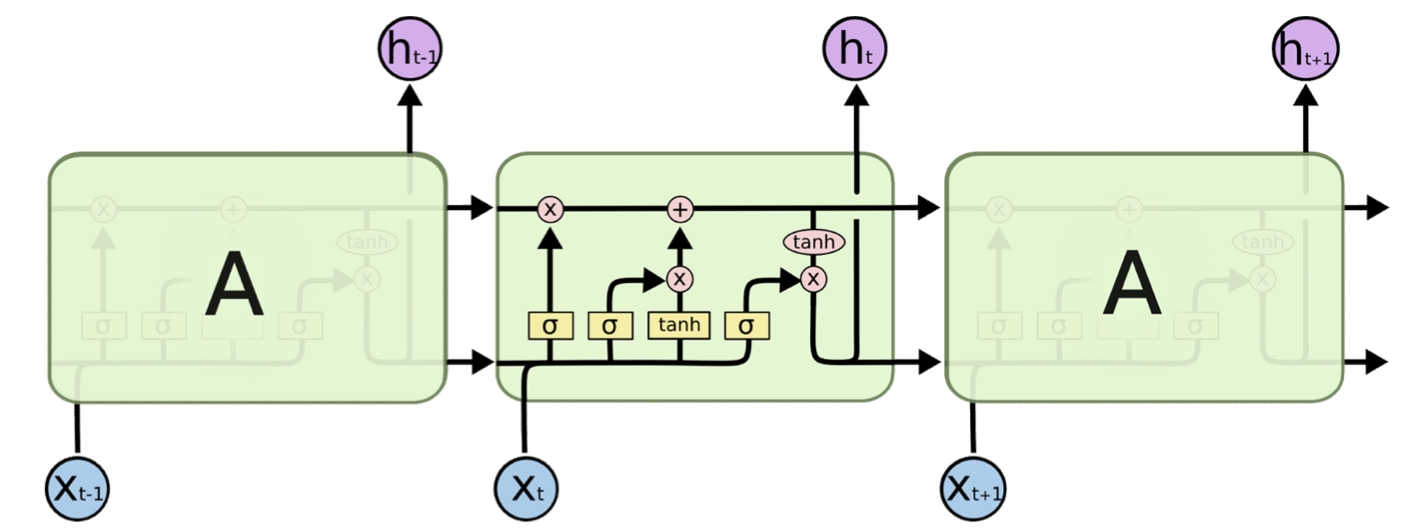
• The $\sigma$ are multiplicative gates that decide if something is important or not

Key component

Remembered cell state

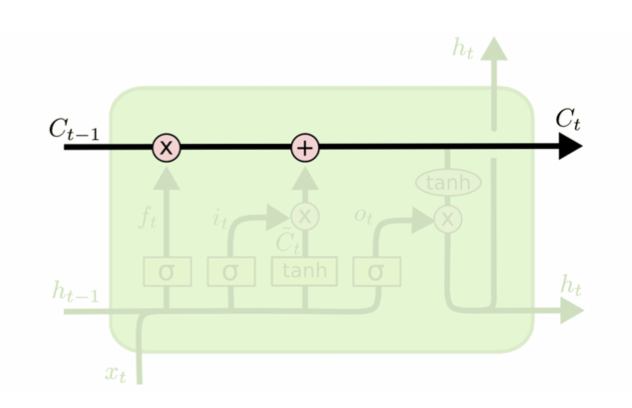
• Mutiply is a switch
  • Should I continue remember or not? (scale up / down)
• Acddition
  • Should I agument the memory?
• $C_t$ is the linear history carried by the constant-error carousel
• Carries information through, only affected by a gate
  • And addition of history, which too is gated..

Gates

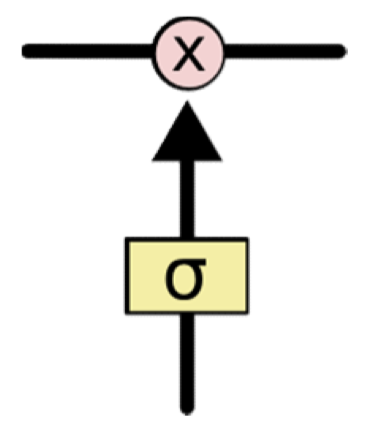
• Gates are simple sigmoidal units with outputs in the range (0,1)
• Controls how much of the information is to be let through

Forget gate

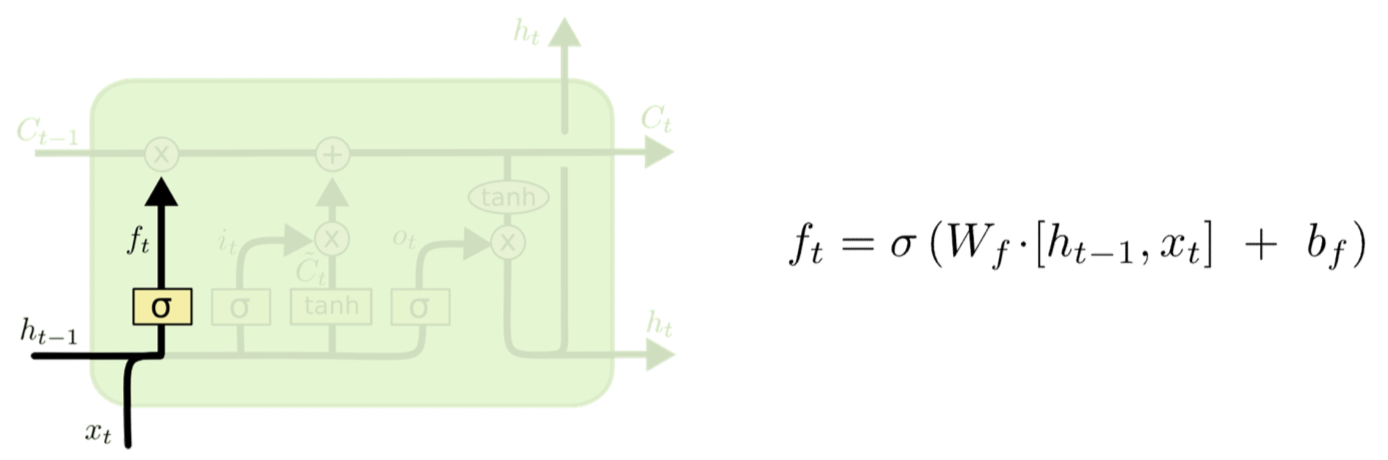
• The first gate determines whether to carry over the history or to forget it
  • More precisely, how much of the history to carry over
  • Also called the “forget” gate
  • Note, we’re actually distinguishing between the cell memory $C$ and the state $h$ that is coming over time! They’re related though
    • Hidden state is compute from memory (which is stored)

Input gate

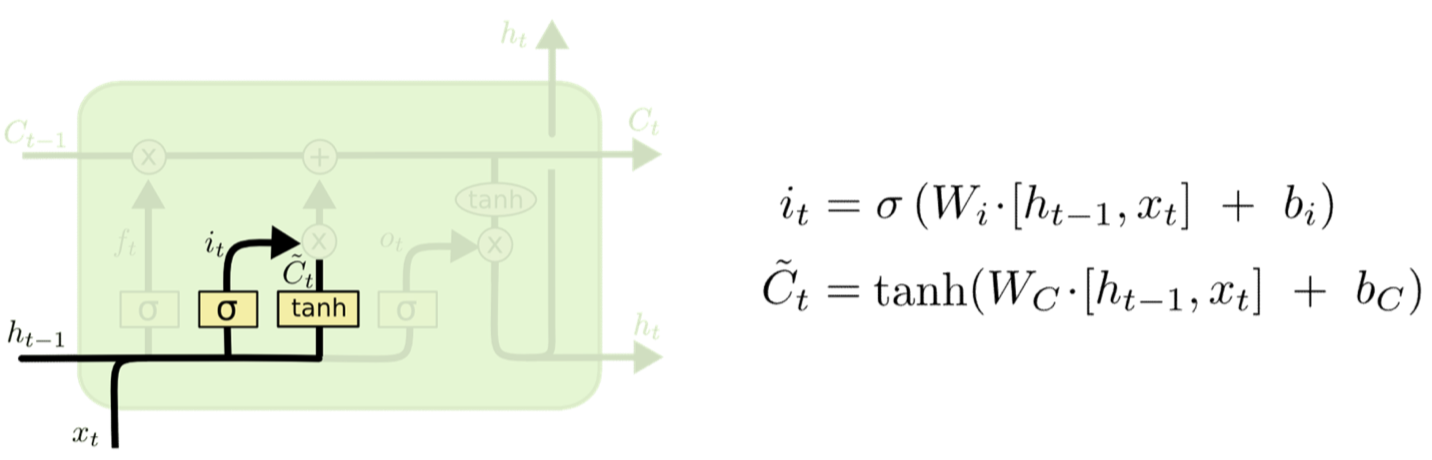
• The second input has two parts
  • A perceptron layer that determines if there’s something new and interesting in the input
    • 「See a curly brace」
  • A gate that decides if its worth remembering
    • 「Curly brace is in comment section, ignore it」

Memory cell update

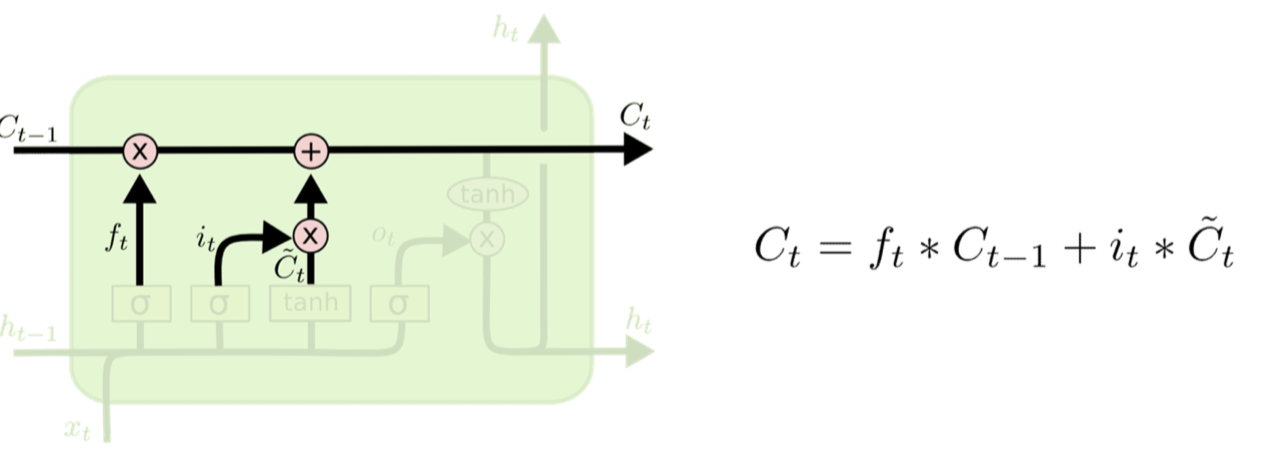
• If something new and worth remembering
  • Added to the current memory cell

Output and Output gate

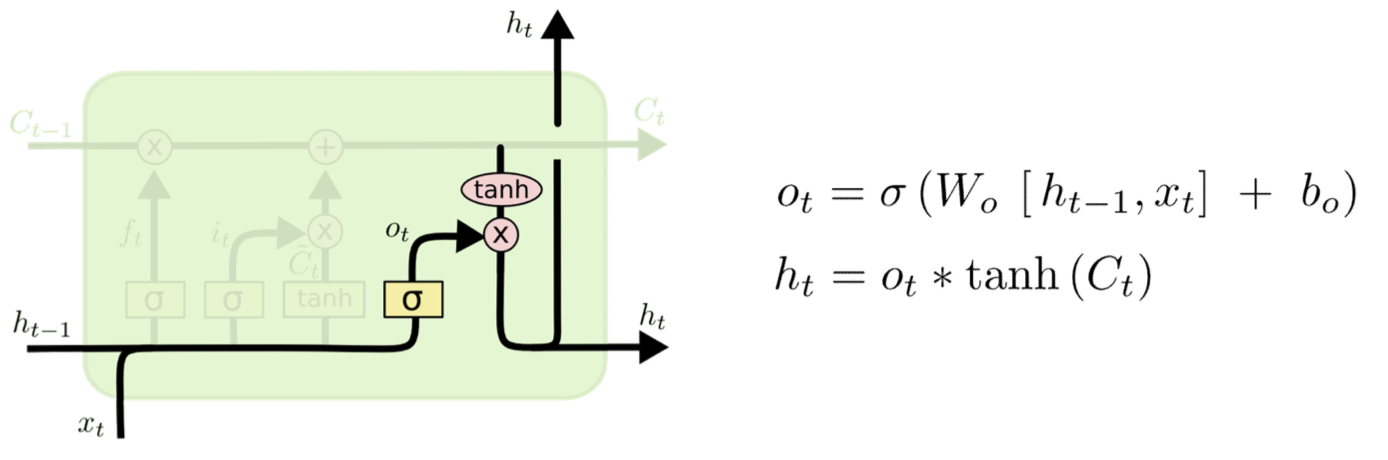
• The output of the cell
  • Simply compress it with tanh to make it lie between 1 and -1
    • Note that this compression no longer affects our ability to carry memory forward
  • Controlled by an output gate
    • To decide if the memory contents are worth reporting at this time

The “Peephole” Connection

• The raw memory is informative by itself and can also be input
  • Note, we’re using both $C$ and $h$

Forward

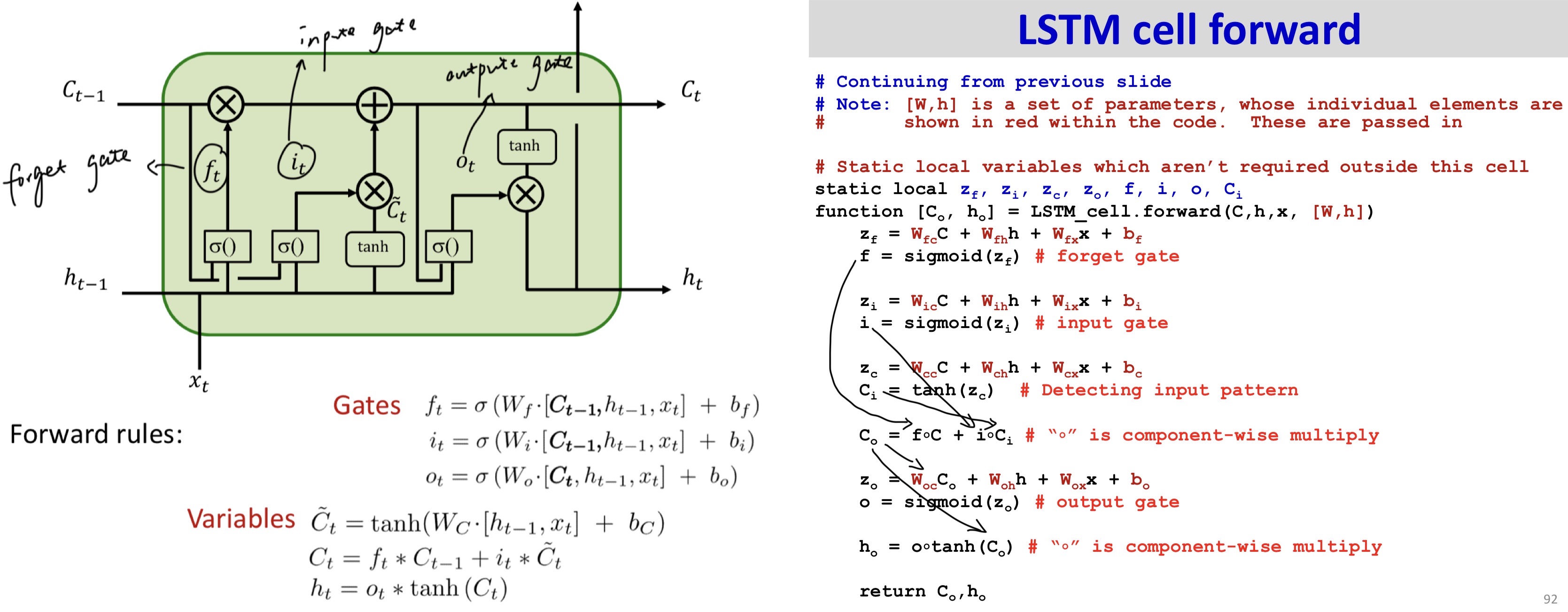
Backward¹

$\begin{array}{l} \nabla_{C_{t}} D i v=&\nabla_{h_{t}} D i v \circ\left(o_{t} \circ \tanh ^{\prime}(.)+\tanh (.) \circ \sigma^{\prime}(.) W_{C o}\right)+ \\\\ &\nabla_{C_{t+1}} D i v \circ\left(f_{t+1}+C_{t} \circ \sigma^{\prime}(.) W_{C f}+\tilde{C}_{t+1} \circ \sigma^{\prime}(.) W_{C i} \circ \tanh (.) \ldots\right) \end{array}$

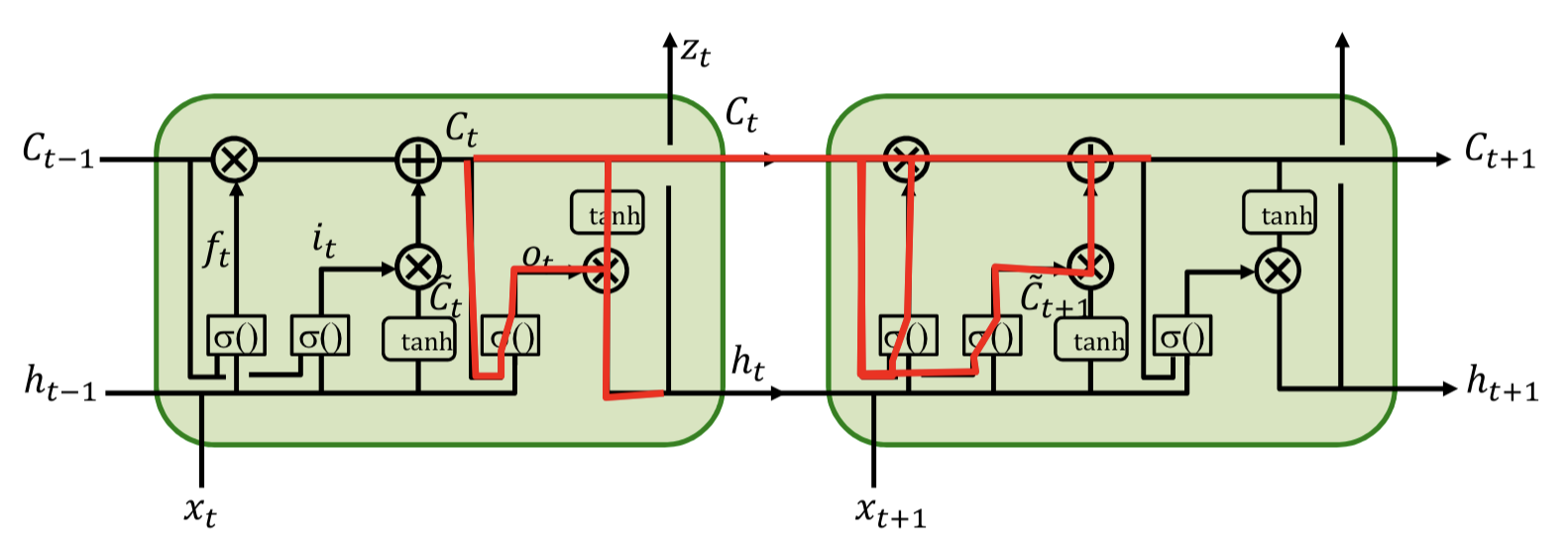
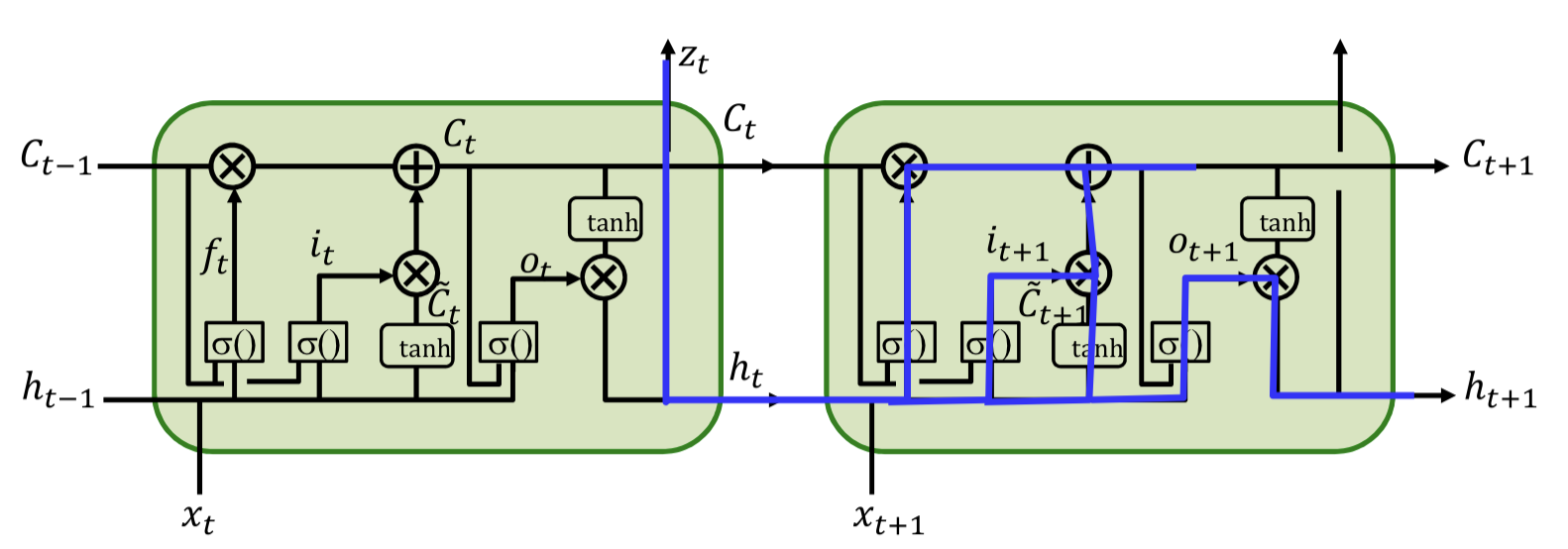$\begin{aligned} \nabla_{h_{t}} D i v=& \nabla_{z_{t}} D i v \nabla_{h_{t}} z_{t}+\nabla_{C_{t+1}} D i v \circ\left(C_{t} \circ \sigma^{\prime}(.) W_{h f}+\tilde{C}_{t+1} \circ \sigma^{\prime}(.) W_{h i}\right)+\\\\ &\nabla_{C_{t+1}} D i v \circ o_{t+1} \circ \tanh ^{\prime}(.) W_{h i}+\nabla_{h_{t+1}} D i v \circ \tanh (.) \circ \sigma^{\prime}(.) W_{h o} \end{aligned}$ And weights?

Gated Recurrent Units

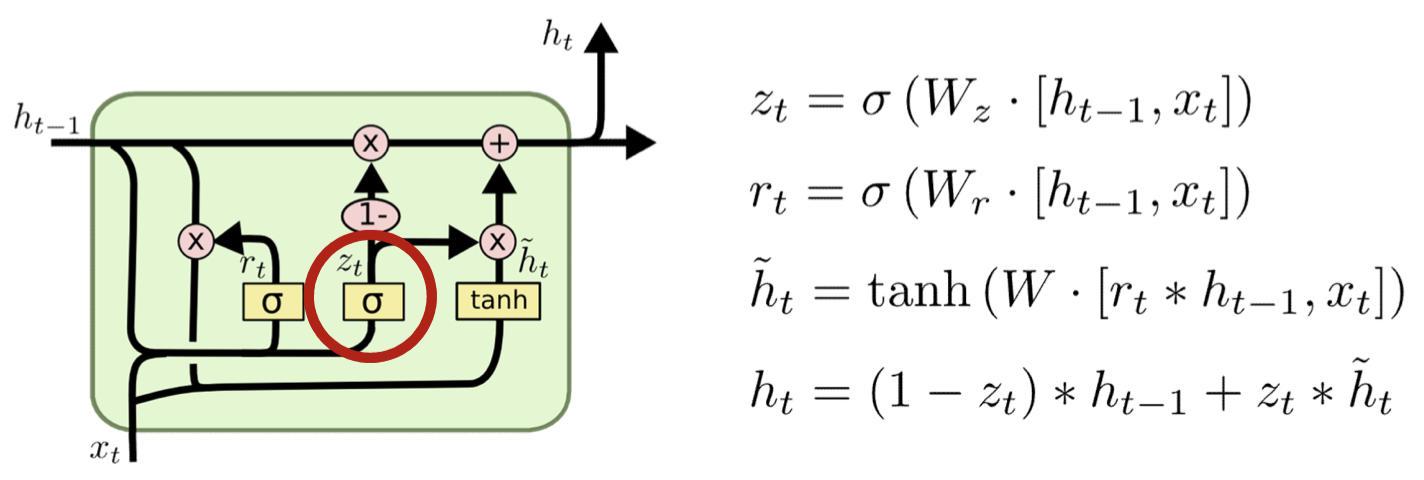
• Combine forget and input gates
  • In new input is to be remembered, then this means old memory is to be forgotten
  • No need to compute twice

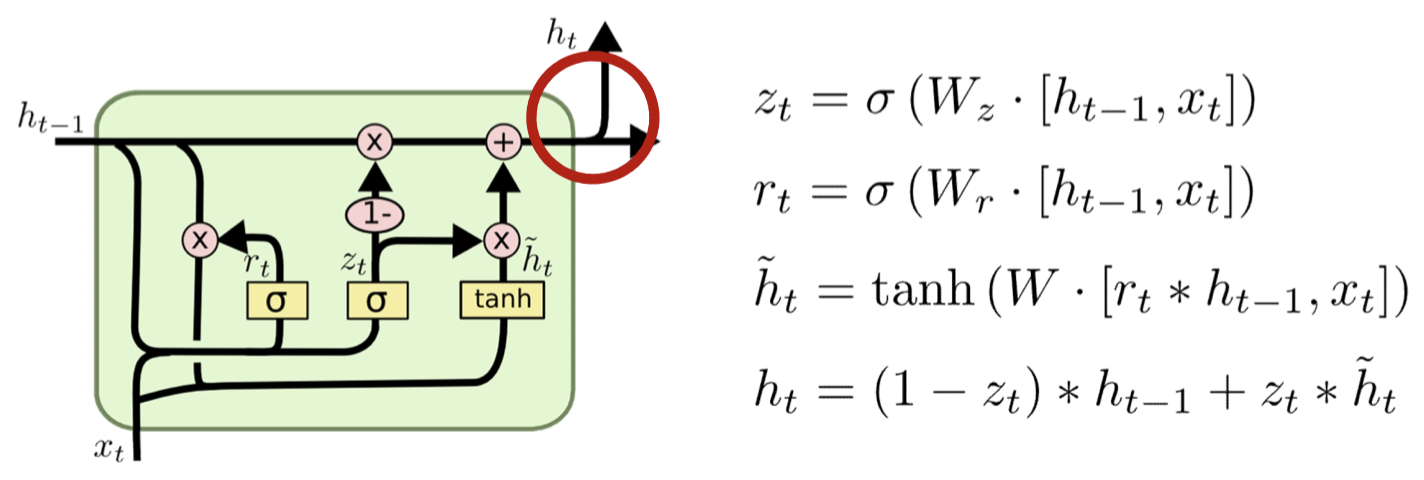
• Don’t bother to separately maintain compressed and regular memories
  • Redundant representation

Summary

• LSTMs are an alternative formalism where memory is made more directly dependent on the input, rather than network parameters/structure
• Through a “Constant Error Carousel” memory structure with no weights or activations, but instead direct switching and “increment/decrement” from pattern recognizers
• Do not suffer from a vanishing gradient problem but do suffer from exploding gradient issue

¹. http://arunmallya.github.io/writeups/nn/lstm/index.html#/ ↩