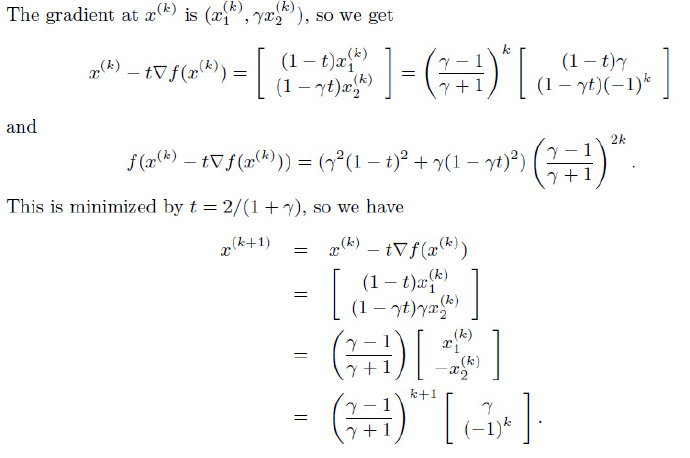本章进入凸优化问题的求解、算法阶段。

无约束优化问题

本文讨论一下无约束问题：

$\min f(x)$

其中，$f$是二次可微凸函数。假定该问题可解，即存在最优解$x^\star$，用$p^\star$表示最优值为：$\inf _xf(x) = f(x^\star)$。

因为$f$可微，则最优点$x^\star$满足以下条件：

$\triangledown f(x^\star)= 0$

在特殊情况下，我们可以通过解析法求解最优性方程，但大多数情况下没有办法求得解析解。因此，最常见的方法是使用迭代法。

我们需要计算点列：$x^{(0)},x^{(1)},..$，使得$k\rightarrow \infty ,f(x^{(k)}) \rightarrow p^\star$。使用$\epsilon$表示容许误差值，当$f(x^{(k)}) - p^\star \le \epsilon$时，算法终止。

例子${p_{438}}$

二次优化

$\min (1/2)x^TPx + q^Tx +r$

很容易我们可以对其求导得到$Px^\star +q= 0$。

因此，若$P$为正定矩阵，则存在唯一解$x^\star = -P^{-1}q$。

若此方程无解，则优化问题无下界。

最小二乘

作为二次优化的特例：

$\min ||Ax - b||^2_2= x^T(A^TA)x - 2(A^Tb)^Tx + b^Tb$

其最优性解为其正规方程：

$A^TAx^\star = A^Tb$

强凸性

强凸是指：

$\triangledown^2 f(x) \succeq mI$

对任意$x\in S$都成立。这里的$\triangledown^2 f(x)$表示Hessian矩阵。

我们可以通过强凸性推导出有意义的方程。

次优性条件

$\begin{aligned} f(y) &=f(x)+\nabla f(x)^{T}(y-x)+\frac{1}{2}(y-x)^{T} \nabla^{2} f(z)(y-x) \\ & \geq f(x)+\nabla f(x)^{T}(y-x)+\frac{m}{2}\|y-x\|_{2}^{2} \end{aligned}$

当$m =0$时，上式变为凸性的基本不等式（一阶可微），当$m\ge 0$时，对$f(y)$的下界得到了更好的估计结果。

对上式进行求导可得：$\triangledown f(x) + m(y-x) = 0$

因此，带入原式可得：

$\begin{aligned} f(y) & \geq f(x)+\nabla f(x)^{T}(y-x)+\frac{m}{2}\|y-x\|_{2}^{2} \\ & \geq f(x)-\frac{1}{2 m}\|\nabla f(x)\|_{2}^{2} \end{aligned}$ 既然该式子对任意$y\in S$都成立，则：

$p^\star \ge f(x) - \frac{1}{2m}||\triangledown f(x)||^2_2$

由于$||\triangledown f(x)||_2 \le (2m\epsilon )^{1/2}$，因此带入可得到次优性条件：

$f(x) - p^\star \le \epsilon$

我们也可以得到$x$与任意最优解$x^\star$之间的距离与$||\triangledown f(x)||_2$的关系：

$||x- x^\star||_2 \le \frac {2}{m}||\triangledown f(x)||_2$

关于$\triangledown^2 f(x)$的上界

由于$||\triangledown^2 f(x)||$的最大特征值是$x$在$S$上的连续函数，因此他在$S$上有界，即存在常数$M$，使得(没懂)：

$||\triangledown^2 f(x)|| \preceq MI$

与上面类似，我们可以得到$p^\star$的上界：

$p^\star \le f(x) - \frac{1}{2M}||\triangledown^2 f(x)||_2^2$

对比$p^\star$的上界：

$p^\star \ge f(x) - \frac{1}{2m}||\triangledown f(x)||^2_2$

下水平集的条件数

从之前的分析我们可以得到：

$mI \preceq ||\triangledown^2 f(x)|| \preceq MI$

因此，比值$M/m$是矩阵$\triangledown^2 f(x)$的条件数的上界，这是影响其计算效率的重要因素。

下降方法

我们讨论的所有方法都是下降方法，只要不是最优点则应该满足：

$f(x^{(k+1)}) < f(x^{(k)})$

而优化点列为：

$x^{(k+1)} = x^{(k)} + t^{(k)}\triangle x^{(k)},\quad t^{(k)} > 0$

由凸性可知$\triangledown f(x^{(k)})^T(y-k^{(k)}) \ge 0$意味着$f(y)\ge f(x^{(k)})$，因此，一个下降方法的搜索方向必须满足：

$\triangledown f(x^{(k)})^T\Delta x^{(k)} <0$

这将作为我们判断后面下降算法的条件之一。

通用下降算法

1. 确定下降方向$\Delta x$
2. 直线搜索。选择步长$t > 0$
3. 修改。$x := x+t\Delta x$
4. 直到满足停止条件

精确直线搜索${p_{444}}$

$t$值是通过沿着射线$\{x+t\triangle x| t\ge 0\}$优化$f$而确定的：

$t = \arg\min_{s\ge0} f(x+s\triangle x)$

当求解式中的单变量优化问题的成本比计算搜索方向的成本低时，采用精确直线搜索。

特殊情况可以用解析的方法确定最优解。

回溯直线搜索

很多时候我们并不需要找到一个最小的$t$，只需要$f$有“足够的”减少即可。

常用的方法为：

1. 给定下降方向$\Delta x$,参数$\alpha\in (0,0.5),\beta\in (0,1)$
2. 设定初始$t = 1$
3. $if \quad f(x+t\triangle x )> f(x) + \alpha t \triangledown f(x)^T \triangle x,then \quad t :=\beta t$

回溯算法从单位步长开始，按比例逐渐减小，直到满足停止条件。

由于$\Delta x$是下降方向，$\triangledown f(x)^T \Delta x< 0$，所以只要$t$足够小，一定有：

$f(x+t\Delta x) \approx f(x) + t\triangledown f(x)^T\Delta x< f(x) + t\alpha\triangledown f(x)^T\Delta x$

因此回溯算法一定会停止。

梯度下降方法

梯度下降利用$\triangle x = -\triangledown f(x)$，是一种自然的选择。

算法过程

1. 给定初始点$x\in dom f$，$\Delta x := \triangledown f(x)$
2. 直线搜索。通过精确或回溯直线搜索确定步长$t$
3. 修改$x:=x+t\Delta x$
4. 直到满足停止准则

收敛性分析

我们可以推导得出：

$f(x^{(k)}) - p^\star \le c^k(f(x^{(0)}) - p^\star)$

其中$c = 1-m/M <1$，因此最多经过$\frac{\log (f(x^{(0)}) -p^\star)/ \epsilon }{\log (1/c)}$次迭代，可以收敛到次优性条件。

例子

$R^2$空间中的二次问题

考虑二次目标函数

$f(x) = \frac{1}{2}(x_1^2 + \gamma x_2^2)$

其中$\gamma$大于0。很容易得到其Hessian矩阵为常数，特征值为1和$\gamma$，因此其下水平集的条件数都等于：

$\frac{\max(1,\gamma)}{\min(1,\gamma)} = \max (\gamma ,1/\gamma )$

我们选取初始点$x^{(0)} = (\gamma ,1)$，可以计算：

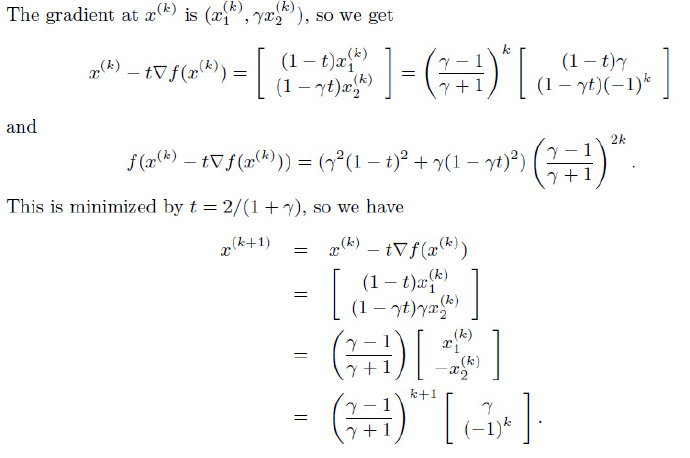
最速下降方法${p_{454}}$

对$f(x+v)$在$x$处进行一阶Taylor展开：

$f(x+v) \approx \hat f(x+v) = f(x) +\triangledown f(x)^Tv$

其中$\triangledown f(x)^Tv$是$f$在$x$在沿着方向$v$的方向导数，若其为负数，则$v$为下降方向。

如何选择$v$使得其方向导数尽可能小（下降最快），我们定义一个规范化的最速下降方向：

$\Delta x_{nsd} = \arg\min \{\triangledown f(x)^T v\space | \space ||v|| =1 \}$

我们也可以考虑将最速下降方向乘以一个特殊的比例因子，从而考虑非规范化的最速下降方向：

$\Delta x_{sd} = ||\triangledown f(x)|| _\star \Delta x_{nsd}$

其中$|| \odot ||_\star$定义为对偶范数（$||z||_\star = \sup\{z^Tx | ||x||\le1\}$）。

对于这种最速下降步径，我们有：

$\nabla f(x)^{T} \Delta x_{s d}=\|\nabla f(x)\|_{\star} \nabla f(x)^{T} \Delta x_{n s d}=-\|\nabla f(x)\|_{\star}^{2}<0$

Newton方法${p_{462}}$

Newton步径

$\Delta x_{nt} = -\triangledown^2 f(x)^{-1}\triangledown f(x)$

由$\triangledown^2f(x)$的正定性可知（凸函数的二阶条件），除非$\triangledown f(x) = 0$，否则：

$\triangledown f(x)^T\Delta x = -\triangledown f(x)^T \triangledown^2 f(x)^{-1}\triangledown f(x) <0$

因此，$\Delta x_{nt}$与负梯度方向为锐角，$\Delta x_{nt}$是下降方向。

可以从以下几个方面来了解Newton步径。

二阶近似的最优解

考虑函数$f$在$x$处的二阶Taylor近似为：

$\hat{f(x+v)} = f(x)+\triangledown f(x)^Tv+\frac{1}{2}v^Tf(x)v$

这是$v$的二次凸函数，在$v =\Delta x_{nt}$处达到最小值。

因此，将$x$加上Newton步径$\Delta x_{nt}$能够极小化$f$在$x$处的二阶近似。

如果函数是二次的，那么使用Newton步径是$f$的精确最优解。若函数近似二次，则$x+ \Delta x_{nt}$是$f$的最优解，即$x^\star$的很好的估计值。

Hessian范数下的最速下降方向

若定义Hessian矩阵$\triangledown^2 f(x)$定义的二次范数，即：

$||u||_{\triangledown^2 f(x)} = (u^T\triangledown^2 f(x)u)^{1/2}$

那么可以通过最速下降方向推出$\Delta x_{nt}$。

线性化最优性条件的解

若我们在$x$附近对最优性条件$\triangledown f(x^\star)=0$进行线性化，可得到：

$\triangledown f(x+v) \approx \triangledown f(x) + \triangledown^2 f(x)v = 0$

其解就是我们的Newton步径。

Newton减量${p_{464}}$

$\lambda(x) = (\triangledown f(x) ^T\triangledown^2 f(x)^{-1}\triangledown f(x))^{1/2}$

$\lambda(x)$称为Newton减量，可以用来设计停止准则。

将$\Delta x_{nt}$带入$f(x+t\Delta x)$得：$f(x+t\Delta x) = f(x)- \frac{1}{2}\triangledown ^Tf(x)\triangledown^2 f(x)^{-1}\triangledown f(x)$

因此：$f(x) - f(x+t\Delta x) = \frac{1}{2}\triangledown ^Tf(x)\triangledown^2 f(x)^{-1}\triangledown f(x) = \frac{1}{2}\lambda(x)^2$

因此，$\lambda^/2$是$f$在$x$处的二阶近似对$f(x) - p^\star$作出的估计。

我们也可以将Newton减量表示为$\lambda = (\Delta x_{nt}^T\triangledown ^2f(x)\Delta x_{nt})^{1/2}$，表明$\lambda$是Newton步径的二次范数，该范数由Hessian矩阵定义。

Newton减量也出现在回溯直线搜索中，因为我们可以得到：

$\triangledown ^Tf(x)\Delta x_{nt} = -\lambda(x)^2$

Newton方法

1. 给定初始点$x \in dom f$，误差阈值$\epsilon >0$
2. 计算Newton步径和减量
3. 停止准则：如果$\lambda^2/2\le \epsilon$，退出
4. 直线搜索，根据回溯直线搜索确定步长$t$
5. 改进：$x:=x + t\Delta x_{nt}$