分类问题

SVM（support vector machine）是一种著名的分类算法。我们学过Logistic回归，但它只能处理简单的线性分类。在现实生活中，很多问题的属性不能简单的用线性分类完成，或者说线性分类的效果不好，这时候我们就要想其他办法。

超平面

我们可以想象这样一个方程：

wTx+b=0w^Tx + b = 0

若这里的xx是二维向量，那么就是我们熟悉的平面方程。若大于二维，则是一个超平面，在SVM中，这个超平面也被称为决策面。

我们的目标就是想找到这样一个决策面，使得样本点能够较好的分布在超平面两侧，这就达到了我们分类的目的。

Part1

首先用一种简单的方法得到优化问题。

分类间隔

很显然，对于样本点来说，这样的决策面肯定不止一个。那么，如何来度量我们分类好坏的标准呢？

在SVM中，我们使用分类间隔来度量，所谓分类间隔，是指保证决策面方向不变且不会错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过则会产生错分现象）。因此，这两条平行线（面）之间的垂直距离就是这个决策面对应的分类间隔。

不同方向的最优决策面通常是不同的，那个具有最大间隔的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为支持向量。

根据我们学习过的平面距离可以得到：

d=∣wT+b∣∣∣w∣∣d = \frac {|w^T + b|}{||w||}

我们首先考虑一个决策面是否能够将所有样本都正确分类的约束。我们可以为每个样本点xix_i加上一个类别标签yi={−1,1}y_i = \{-1,1\}，假如我们的决策面方程能够完全正确的对所有样本点进行分类，则可以得到：

f(x)={wTxi+b>0 for yi=1wTxi+b<0 for yi=−1 f(x)=\left\{\begin{aligned}w^Tx_i + b >0 \space for \space y_i = 1 \\w^Tx_i + b <0 \space for \space y_i = -1\end{aligned}\right.

如果我们要求再高一点，假设决策面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到决策面的距离为d，那么公式可以进一步写成：

f(x)={(wTxi+b)/∣∣w∣∣≥d ∀yi=1(wTxi+b)/∣∣w∣∣≤−d ∀yi=−1 f(x)=\left\{\begin{aligned}(w^Tx_i + b )/||w||\ge d \space \forall y_i = 1 \\ (w^Tx_i + b )/||w||\le -d \space \forall y_i = -1\end{aligned}\right.

对公式重写（两边同时除以d）：

f(x)={wdTxi+bd≥1 for yi=1wdTxi+bd≤1 for yi=−1wd=w∣∣w∣∣d,bd=b∣∣w∣∣d f(x)=\left\{\begin{aligned}w_d^Tx_i + b_d \ge1 \space for \space y_i = 1 \\w_d^Tx_i + b_d \le1 \space for \space y_i = -1\end{aligned}\right. \quad w_d = \frac{w}{||w||d},b_d = \frac {b}{||w||d}

由于wdw_d与ww并没有本质差别，因此不再做区分，我们的目标是想要在正确分类的情况下使得分类间隔最大化，即max{d}max \{d\}，也就是min⁡∣wdTxi+bd∣∣∣wd∣∣≥1∣∣wd∣∣\min {\frac{|w_d^Tx_i +b_d|}{||w_d||}} \ge \frac{1}{||w_d||}，也等价于min{12∣∣wd∣∣2}min \{ \frac {1}{2} ||w_d||^2\}。

因此，我们得到我们问题的总描述：

min⁡12∣∣w∣∣2\min \frac {1}{2} ||w||^2

s.t.yi(wTxi+b)≥1,i=1,...,ns.t. \quad y_i(w^Tx_i +b)\ge1,i=1,...,n

Part2

使用margin得到优化问题。

margins

  • Functional margins
    • γ(i)^=y(i)(wTx+b)\hat{\gamma^{(i)}} = y^{(i)}(w^Tx + b)
    • 这个函数可以用来衡量confident和correct
    • 如果分类正确，那么该函数始终是正数，且离决策边界越远，值越大，也就越confident
    • 如果分类错误，那么该函数是负数
    • 因此，我们的目标是找到最小的margin，也就是 γ^=min⁡γ(i)^\hat{\gamma} = \min \hat{\gamma^{(i)}}
  • Geometric margins
    • Functional margins有一个很大的问题在于，如果我等比例的scale w,bw,b，那么该值就一定会增大。但此时对于margin来说并没有提升，因此无法直接用来衡量。
    • 我们新定义一个Geometric margins，可以认为是一个相对的大小：
      • γ(i)=y(i)(w∣∣w∣∣Tx+b∣∣w∣∣)\gamma^{(i)} = y^{(i)}(\frac{w}{||w||}^Tx + \frac{b}{||w||})
      • 实际上，γ=γ^∣∣w∣∣\gamma = \frac{\hat{\gamma}}{||w||}
    • 我们的目标不变:
      • γ=min⁡γ(i)\gamma = \min \gamma^{(i)}
    • 问题表述为：
      • max⁡γ\max \gamma
      • s.t.y(i)(wTx(i)+b)≥γs.t.\quad y^{(i)}(w^Tx^{(i)} + b )\ge \gamma
      • ∣∣w∣∣=1||w|| = 1
    • 很容易证明，这时候无论w,bw,b 如何 scale，都不会影响margins了。（类似于normalization）
    • 但由于有∣∣w∣∣=1||w|| = 1的条件，类似于在球面上进行优化，不是一个凸优化问题，很难求解。

Optimal margin classifier

我们的目标是最大化geometry margins，因此可以将原问题写为：

max⁡γ∣∣w∣∣\max \frac{\gamma}{||w||}

s.t.y(i)(wTx(i)+b)≥γs.t. y^{(i)}(w^Tx^{(i)} + b) \ge \gamma

但这依然不容易求解，联想到，我们已经使得无论w,bw,b 如何 scale，都不会影响最终的值，因此，总是可以使w,bw,b 满足γ=1\gamma = 1，因此，我们的目标函数可以写为max⁡1∣∣w∣∣\max \frac{1}{||w||}。注意到，最大化1∣∣w∣∣\frac{1}{||w||}和最小化∣∣w∣∣2||w||^2是一回事情（更容易求导），因此，我们将原问题转为了凸优化问题（没有局部最优值）：

min⁡12∣∣w∣∣2\min \frac {1}{2} ||w||^2

s.t.yi(wTxi+b)≥1,i=1,...,ns.t. \quad y_i(w^Tx_i +b)\ge1,i=1,...,n

线性可分情况

拉格朗日函数

这是一个有约束条件的极值问题，因此可使用拉格朗日函数表达：

L(w,b,a)=12∣∣w∣∣2−∑i=1nαi(yi(wTxi+b)−1)L(w,b,a) =\frac {1}{2} ||w||^2 - \sum\limits _{i=1}^n \alpha_i(y_i(w^Tx_i +b)-1)

我们令αi≥0,θ(w)=maxai≥0L(w,b,a)\alpha_i \ge 0,\theta(w) = {max}_{a_i \ge 0} L(w,b,a) 。容易验证：当某个约束条件不满足时，例如yi(wTxi+b)<1y_i(w^Tx_i +b)<1，则有θ(w)=∞\theta(w) = \infty （只要令αi=∞\alpha _i = \infty而当所有约束都满足时，则有θ(w)=12∣∣w∣∣2\theta(w) = \frac {1}{2} ||w||^2，即为最初要最小化的量。

这样，我们就使用拉格朗日函数将所有约束条件集中到一个函数中，目标函数变成了：

min⁡w,bθ(w)=min⁡w,bmax⁡αi≥0L(w,b,a)=p∗\min\limits_{w,b}\theta(w) = \min\limits_{w,b} \max\limits_{\alpha_i\ge 0}L(w,b,a) = p^*

这里用p∗p^*表示这个问题的最优解，且与最初的问题是等价的，但如果直接面对这个函数，有w,bw,b两个参数，并且α\alpha还是不等式约束，不好求解。那么我们可以转化为对偶问题：

max⁡αi≥0min⁡w,bL(w,b,a)=d∗\max\limits_{\alpha_i\ge 0}\min\limits_{w,b} L(w,b,a) = d^*

这个新问题的最优解表示为d⋆d^\star，且有d⋆≤p⋆d^{\star} \le p^{\star}（总是成立）,在某些情况下这两者相等，因此可以求解对偶问题来间接求解原始问题。

KKT条件

由于对偶问题和原始问题有 d⋆≤p⋆d^{\star} \le p^{\star} 的关系，但我们更希望取等号，这样我们就可以利用对偶问题来求得原问题的最优解。

而满足这种条件的约束称为KKT条件。

首先重新定义一下凸优化问题：

min⁡f(w)\min f(w)

s.t.gi(w)≤0s.t. \quad g_i(w) \le 0

hi(w)=0h_i(w) = 0

拉格朗日函数可以表示为：L(w,α,β)=f(w)+∑αigi(w)+∑βih(w)L(w,\alpha,\beta) = f(w) + \sum \alpha_i g_i(w) + \sum \beta_i h(w)

KKT条件可以表示为：

∂∂wiL(w∗,α∗,β∗)=0\frac{\partial}{\partial w_i}L(w^*,\alpha^*,\beta^*) = 0

∂∂βiL(w∗,α∗,β∗)=0\frac{\partial}{\partial \beta_i}L(w^*,\alpha^*,\beta^*) = 0

αi∗gi∗(w∗)=0\alpha_i^* g_i^*(w^*) = 0

gi(w∗)≤0g_i(w^*) \le 0

α∗≥0\alpha^* \ge 0

其中第三个条件被称为dual complementarity condition，也就是说，只有在gi⋆(w⋆)=0g_i^{\star}(w^{\star}) = 0时α≠0\alpha \ne 0，也就是真正作为support vector，在后面的SMO中会有帮助。

对偶问题求解

我们需要求解的方程为：

max⁡αi≥0min⁡w,bL(w,b,a)=d∗\max\limits_{\alpha_i\ge 0}\min\limits_{w,b} L(w,b,a) = d^*

首先固定α\alpha，对w,bw,b求导数：

∂L∂w=0⇒w=∑i=1naiyixi\frac{\partial L }{\partial w} = 0 \Rightarrow w =\sum\limits_{i=1}^{n}a_iy_ix_i

∂L∂b=0⇒∑i=1naiyi=0\frac{\partial L }{\partial b} = 0 \Rightarrow\sum\limits_{i=1}^{n}a_iy_i = 0

将上面的结果带到L(w,b,a)L(w,b,a)中可得：

L(w,b,a)=12∥w∥2−∑i=1nαi(yi(wTxi+b)−1)=12∥w∥2−∑i=1naiyiwTxi−∑i=1naiyib+∑i=1nai=−12∑i,j=1naiajyiyjxT−ixj+∑i=1nai \begin{aligned} L(w, b, a) &=\frac{1}{2}\|w\|^{2}-\sum_i=1^{n} \alpha_ i\left(y_ i\left(w^{T} x_ i+b\right)-1\right) \\ &=\frac{1}{2}\|w\|^{2}-\sum_ i=1^{n} a_ i y_ i w^{T} x_ i-\sum_ i=1^{n} a_ i y_ i b+\sum_ i=1^{n} a_ i \\ &=-\frac{1}{2} \sum_ i, j=1^{n} a_i a_ j y_ i y_ j x^{T}-i x_ j+\sum_ i=1^{n} a_ i \end{aligned} 这样，我们的目标函数就变为：

max⁡α∑i=1nai−12∑i,j=1naiajyiyjxiTxj\max\limits_{\alpha} \sum\limits _{i= 1}^n a_i-\frac {1}{2} \sum\limits_{i,j = 1}^n a_ia_jy_iy_jx^T_ix_j

s.t.ai≥0,i=1,...,and∑i=1naiyi=0s.t. \quad a_i\ge0,i=1,..., and \sum\limits_{i=1}^{n}a_iy_i = 0

这样，我们的目标就变成了求α\alpha，从而可以求出：

w=∑i=1naiyixiw =\sum\limits_{i=1}^{n}a_iy_ix_i

b=−max⁡i:yi=−1wTx+min⁡i:yi=1wTxi2b = - \frac {\max _{i:y_i = -1} w^Tx + \min_{i:y_i = 1}w^Tx _i}{2}

求α\alpha 比直接求w,bw,b简单多了，其中SMO算法是目前最常用的，我们之后再说。

我们目前的分类函数为f(x)=wTx+bf(x) = w^Tx+b，带入：

f(x)=(∑αiyixi)Tx+b=∑αiyi(xi,xj)+b\begin{aligned} f(x) &=\left(\sum \alpha_i y_i x_ i\right)^{T} x+b \\ &=\sum \alpha_i y_i\left(x_i, x_j\right)+b \end{aligned}

注意，这里的(xi,xj)(x_i,x_j)表示向量乘积，因此，对于新点xx，只需要计算它与训练数据点的内积即可。这一点在之后的kernel函数中也会使用。

同时，如果我们的αi≠0\alpha_i \ne 0，说明该变量对ww有贡献，因此为support vector（可以直接从KKT条件中的function margin=1得到）。

线性不可分情况

核函数

  • 将attributes -> feature 的过程定义为feature mapping，例如
    • ϕ(x)=[xx2x3]\phi(x) = \begin{bmatrix}x\\x^2 \\ x^3\end{bmatrix}
    • 因此，我们想从feature中进行学习，而不是原始的attributes。而注意到，我们对样本的预测只与内积有关，因此可以定义Kernel：K(x,z)=ϕ(x)Tϕ(z)K(x,z) = \phi(x)^T\phi(z)
    • 这样，在原始算法中的所有内积都用Kernel代替，这样就实现了从feature中学习
  • 这里最值得注意的是，为什么我们不直接学习feature的表示，而要学习kernel呢？
    • 因为kernel的计算代价可能远远小于提取feature
    • 例如，如果K(x,z)=(xTz+c)dK(x,z) = (x^Tz +c)^d，则对应于Cn+dnC_{n+d}^n个feature space，而对于计算kernel来说，复杂度只有O(n)O(n)
    • 这种kernel的思想并不仅仅适用于SVM，只要有内积的形式，都可以使用，可以大大减少feature空间的维度
  • 直觉来说，如果ϕ(x)\phi(x)和ϕ(z)\phi(z)越相近，则我们希望得到的K(x,z)K(x,z)越大，反之越小
  • 例如Gaussian kernel：K(x,z)=exp⁡(−∣∣x−z∣∣2wσ2)K(x,z) = \exp(-\frac{||x-z||^2}{w\sigma^2})
    • correspond to an infinite dimensional feature mapping

正则化&不可分

  • 当我们用ϕ\phi将数据映射到高维特征空间，并不能提高线性可分的likelihood。同时，如果样本中存在outlier，会大大影响我们分类的效果和margin的大小。
  • 因此，我们希望模型能够对outlier不敏感，加上正则项(l1l_1正则化）：
    • min⁡γ,w,b12∣∣w∣∣2+C∑i=1mεi\min_{\gamma,w,b} \frac{1}{2}||w||^2 + C\sum\limits_{i=1}^m\varepsilon_i
    • s.ty(i)(wTx(i)+b)≥1−εis.t\quad y^{(i)}(w^Tx^{(i)} + b) \ge 1- \varepsilon_i
    • εi≥0\varepsilon_i \ge 0
  • CC越大，对误分类对惩罚越大，模型越复杂，泛化能力差。
  • 这样，我们的拉格朗日问题就变为：
    • L(w,b,ε,α,r)=12wTw+C∑i=1mεi−∑i=1mαi[y(i)(xTw+b−1+εi)]−∑i=1mriεiL(w,b,\varepsilon,\alpha,r) = \frac{1}{2} w^Tw + C\sum\limits_{i=1}^m\varepsilon _i - \sum\limits_{i=1}^m\alpha_i[y^{(i)}(x^Tw + b - 1 +\varepsilon_i)] - \sum\limits_{i=1}^m r_i \varepsilon_i
  • 通过同样的方法，可以得到拉格朗日对偶问题为：
    • max⁡α∑i=1nai−12∑i,j=1naiajyiyj(xi(i),x(j))\max\limits_{\alpha} \sum\limits _{i= 1}^n a_i-\frac {1}{2} \sum\limits_{i,j = 1}^n a_ia_jy_iy_j(x^{(i)}_i,x^{(j)})
    • s.t.0≤α≤Cs.t. \quad 0\le \alpha \le C
    • ∑i=1mαiy(i)=0\sum\limits_{i=1}^m \alpha_i y^{(i)} = 0
  • 根据KKT条件，我们可以得到
    • αi=0⇒y(i)(wTx(i)+b)≥1\alpha_i = 0 \quad \Rightarrow\quad y^{(i)}(w^Tx^{(i)} + b) \ge 1
    • αi=C⇒y(i)(wTx(i)+b)≤1\alpha_i = C \quad \Rightarrow\quad y^{(i)}(w^Tx^{(i)} + b) \le 1
    • 0<αi<C⇒y(i)(wTx(i)+b)=10<\alpha_i < C \quad \Rightarrow\quad y^{(i)}(w^Tx^{(i)} + b) = 1

SMO算法

我们已经将SVM的基本问题从attributes空间通过kernel转到feature空间，同时定义了有正则项的对偶函数，最后剩下的就是如何求解了。

Coordinate ascent

我们之前已经熟悉了gradient ascent和Newton's method两种优化算法，现在介绍一种新的优化方法。

假设我们的优化目标是max⁡αW(α1,α2,...,αm)\max\limits_{\alpha} W(\alpha_1,\alpha_2,...,\alpha_m)

那么，我们按照一定的order对某些变量依次进行更新（从启发式算法角度考虑，我们的更新order是从希望更新的参数变化最大的开始）：

αi:=arg⁡max⁡αi^W(α1,α2,..αi.,αm)\alpha_i := \arg\max_{\hat{\alpha_i}} W(\alpha_1,\alpha_2,..\alpha_i.,\alpha_m)

这种优化算法非常有效，收敛得很快。

SMO

max⁡α∑i=1nai−12∑i,j=1naiajyiyj(x(i),x(j))\max\limits_{\alpha} \sum\limits _{i= 1}^n a_i-\frac {1}{2} \sum\limits_{i,j = 1}^n a_ia_jy_iy_j(x^{(i)},x^{(j)})

s.t.0≤α≤Cs.t. \quad 0\le \alpha \le C

∑i=1mαiy(i)=0\sum\limits_{i=1}^m \alpha_i y^{(i)} = 0

我们如果直接对满足约束条件的优化问题使用coordinate ascent，则会发现，如果我们需要更新的α1\alpha_1，在约束条件下，没有办法得到更新后的值。这是因为：

α1y(1)=−∑i=2mαiy(i)\alpha_1y^{(1)} = - \sum\limits_{i=2}^m \alpha_i y^{(i)}

因此，解决该问题，至少需要我们同时更新两个值。

首先，如果我们同时更新α1,α2\alpha_1,\alpha_2，则约束条件为：

α1y(1)+α2y(2)=−∑i=3mαiy(i)=ε\alpha_1 y^{(1)} + \alpha_2y^{(2)} = -\sum\limits_{i=3}^m \alpha_i y^{(i)} = \varepsilon

实际上，由于0≤α≤C0\le \alpha \le C，因此可以更进一步得到其范围：

p2

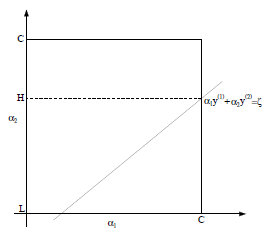
带入目标函数为：

W(α1,α2,...,αm)=W((ε−α2y(2)),α2,...,αm)W(\alpha_1,\alpha_2,...,\alpha_m) = W((\varepsilon - \alpha_2y^{(2)}),\alpha_2,...,\alpha_m)

实际上，根据我们之前写的WW的具体形式，这里就是一个关于α2\alpha_2的二次型函数：aα22+bα2+ca \alpha_2^2 + b\alpha_2 + c，同时满足某些约束L≤α2≤HL\le \alpha_2 \le H，这样我们很容易就可以求得更新后的α2\alpha_2的值。

这样，我们就可以按照coordinate ascent的方式依次更新所有的参数，直到收敛。

Reference

  1. 从另一个方面看SVM的损失函数和正则项
  2. Regularization perspectives on support-vector machines

results matching ""

    No results matching ""