最小二乘法大家都很熟悉了，今天以向量投影的角度重新认识它。

引入

回到解方程组$Ax = b$。

若$Ax = b$ 有解，则$b\in C(A)$。

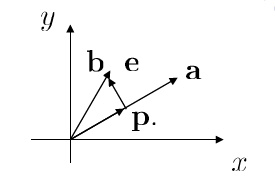
若$Ax = b$ 有解，则$b\notin C(A)$，转化为问题求：$\hat{x}$使得||$A\hat{x} - b$||最小，即$min_{x\in R^n}||A\hat{x}-b||$的最小值点。

由上一讲可知，最小值其实就是$e = b- A\hat x$，即误差向量。在空间中表示为$b$ 在$C(A)$上的投影。

因此，我们可以求得投影向量$p = A\hat x$，然后根据$e \perp C(A)$得到法方程组：$A^TA\hat x= A^Tb$。

法方程组有几个重要的性质：

1. 法方程组总有解（无论A是否列满秩）。

2. $A^TA\hat x = A^Tb$的解可能有无数多个，但$p = A\hat x$唯一。

直线拟合

首先我们来看最常见的直线拟合。

我们想得到目标直线$\hat y = a + bx, e_i = y_i - \hat y_i$。

给定数据$\{(x_1,y_1,...(x_n,y_n)\}$。寻找直线$y=C+Dx$，使得误差最小:

$E(C,D)=[y_1-(C+Dx_1)]^2+ .... +[y_n-(C+D_n)]^2$

即向量$\begin{pmatrix}y_1-(C+Dx_1)\\\\ ...\\\\ y_n-(C+Dx_n)\end{pmatrix}$的长度最小。

令$A = \begin{pmatrix}1 & \ x_1 \\\\...& ...\\\\\ 1& x_n \end{pmatrix}$，$b = \begin{bmatrix}y_1\\ ...\\ y_n \end{bmatrix}$，$\hat x = b = \begin{bmatrix}\hat C\\ \hat D\end{bmatrix}$。即求解$\hat x$ 使得$||b-A\hat{x}||$最小。

利用之前的结论，$A^TA\hat x= A^Tb$，带入即可得：

$\hat C = \overline y - \hat D \overline x, \space \hat D = \frac{\sum\limits_{i=1}^{n}(x_i - \overline x)(y_i - \overline y)}{\sum\limits_{i=1}^{n} (x_i - \overline x)}$

直线$y = \hat C + \hat Dx$称为最小二成直线。

因此，我们只需要求法方程组，即可求得直线的所有参数。

微积分

曲线拟合与直线类似，只是多了几个参数而已，在此不做介绍。

我们现在可以说明法方程组也来自微积分。令：

$f(x_1,...,x_n) = || Ax = b||^2=(Ax-b)^T(Ax-b)$

则$\frac{\partial f}{\partial X} = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\\\...\\\\ \frac{\partial f}{\partial x_n} \end{pmatrix} = 2A^TAX - 2A^Tb$。

若$\hat x$ 满足$min_{x\in R^n}||A\hat{x}-b||$，则$\frac{\partial f}{\partial X}$一定是极值点。因此可得：$A^TA\hat x= A^Tb$。