本节在共轭转置的基础上介绍奇异值和奇异值分解，为严格证明过程。

谱分解

共轭转置

矩阵$A$的共轭转置$A^H$（又称Hermite共轭、Hermite转置）定义为：

$A^H = (\bar A) ^T = \bar {A^T}$

酉矩阵

设$U \in C^{n\times n}$阶复方阵，若$U^HU = I$，则称$U$是酉矩阵。

Hermite矩阵

设$A\in C^{n\times n}$，如果$A^H = A$，那么$A$为Hermite矩阵；

如果$A^H = - A$，则$A$为反Hermite矩阵。

Schur定理

任何一个$n$阶复矩阵都酉相似于一个上三角矩阵，则存在一个$n$阶酉矩阵$U$和一个$n$阶上三角矩阵$R$使得：

$U^HAU = R$

其中$R$的对角元是$A$的特征值。

正规矩阵

设$A \in C^{n\times n}$，如果：

$AA^H = A^HA$

则称$A$为正规矩阵。

可以证明，对角矩阵，Hermite矩阵，反Hermite矩阵，酉矩阵都是正规矩阵。

酉相似条件

$n$阶矩阵$A$酉相似于一个对角矩阵的充分必要条件为$A$是正规矩阵。

因此，若$A$是$n$阶Hermite矩阵，则$A$必酉相似与实对角矩阵，即存在$n$阶酉矩阵$U$使得：

$U^HAU = \Lambda$

因为$A^H = A$，则$\Lambda ^H = \Lambda$，因此$\Lambda$是实对角矩阵。

谱分解

Hermite的谱分解式

由上文可知，若$A$为Hermite矩阵，则：

$U^HAU = \Lambda$

奇异值分解

奇异值定义

设$A \in C^{n\times n}$，如果存在非负实数$\sigma$和非零向量$u\in C^n,v\in C^m$，使得：

$Au = \sigma v , A^H v = \sigma u$

则称$\sigma$ 为$A$的奇异值，$u$和$v$分别称为$A$对应于奇异值$\sigma$的右奇异向量和左奇异向量。

$A^H A u = \sigma A^H v = \sigma ^2 u$

因此$\sigma ^2$是$A^HA$的特征值，也是$AA^H$的特征值，而$u$和$v$分别是$A^HA$和$AA^H$对应于$\sigma ^2$的特征向量。

引理

1. 设$A \in C^{m\times n}$，则

   • $rank(A^HA) = rank(AA^H ) = rank(A)$

2. 设$A \in C^{m\times n}$，则

   • $A^HA$与$AA^H$的特征值均为非负实数
   • $A^HA$与$AA^H$的非零特征值相同，并且非零特征值个数等于$rank(A)$

定理

1. 设$A$是正规矩阵，则$A$的奇异值为$A$的特征值的模。

2. 设$A$是$m\times n$矩阵，且$rank(A) = r$，则存在$m$阶酉矩阵$U$和$n$阶酉矩阵$V$使得：

   • $U^H AV = \begin{pmatrix}\sum &0 \\\\0 & 0\end{pmatrix}$

   • $\sum = diag(\sigma_1,...,\sigma_r)$，且$\sigma_1 \ge ...\ge \sigma_r > 0$为矩阵$A$的奇异值

   • 这个式子就被称为奇异值分解。

证明

易得$A^HA$为Hermite矩阵，$A^HA$的特征值$\lambda^2\ge\lambda^2\ge...>0$

由Schur定理可得，存在$n$阶酉矩阵，使得：

$U^H(A^HA)V =\begin{pmatrix}\sum^2 &0 \\\\0 & 0\end{pmatrix}$

将$V$分解为$V = (V_1,V_2),V_1 = C^{n\times r},V_2 = C^{n\times(n-r)}$

重写上式为：

$A^HA(V_1,V_2)= (V_1,V_2)\begin{pmatrix}\sum^2 &0 \\\\0 & 0\end{pmatrix}$

因此，$AV_2 = 0,U_1 = AV_1\sum^{-1},$则$U_1$是酉矩阵：$U_1^HU_1 = I$。

因此$U_1$的前$r$列两两正交且为单位向量，将其扩充为$C^m$的标准正交基，$U_2 = (u_{r+1},...,u_m)$

则$U = (U_1,U_2)$是$m$阶酉矩阵，$U_1^HU_1 = I,U_2^HU_1 = 0$

$U^H(A^HA)V = U^H (AV_1,AV_2) = \begin{pmatrix}U_1^H\\\\U_2^H \end{pmatrix} (U_1\sum,0) = \begin{pmatrix}\sum^2 &0 \\\\0 & 0\end{pmatrix}$

因此：

$A = U\begin{pmatrix}\sum^2 &0 \\\\0 & 0\end{pmatrix} V^H$

$V$为$A^HA$的r个非零特征值对应的特征向量并单位化

$U$为$AA^H$的r个非零特征值对应的特征向量并单位化

奇异值分解的几何意义

我们观察SVD这个式子：

$A = U\sum V^T$

我们知道，若对一个向量乘以正交矩阵，相当于对其进行旋转变换（不改变长度和比例），而乘以一个对角矩阵，则相当于对其进行伸缩变换，因此，我们对线性变换$X \rightarrow AX$，$X$为单位元上的点，其线性变化可以表示为：

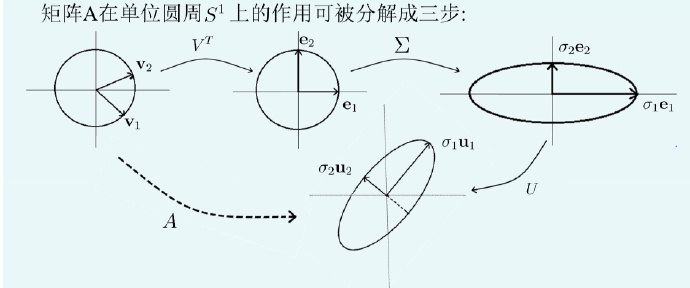
一般的，设秩为$r$的$m\times n$矩阵$A$有SVD:$A = U\sum V^T$，从$R^n$到$R^m$的线性变换$X \rightarrow AX$可以看成是以下三步的复合：

1. $R^n$中的旋转$X \rightarrow V^TX$

2. $R^n$中的向量$V^TX$的前$r$个分量做伸缩，其余分量变为零：

   • $V^TX \rightarrow \sum V^TX$

3. 再在$R^m$中做旋转$\sum V^TX \rightarrow U\sum V^TX$

SVD的性质和本质

1. 正交矩阵$U$的前$r$列是$C(A)$的一组标准正交基。

2. 正交矩阵$U$的后$m-r$列是$N(A^T)$的一组标准正交基。

3. 正交矩阵$V$的前$r$列是$C(A^T)$的一组标准正交基。

4. 正交矩阵$V$的后$n-r$列是$N(A)$的一组标准正交基。

5. 设$|\lambda|_{max}$是矩阵的特征值的模长最大值，则：

   • $\sigma_1 \ge |\lambda |_{max},\sigma_1 \ge |a_{ij}|$

   • 即最大奇异值大于等于特征值模长的最大值，也大于等于矩阵的元素

6. 矩阵$A$列满秩 $\Leftrightarrow$$A$的奇异值均非零

思考

1. 对于正定对称矩阵而言，奇异值分解和对角化相同

2. 特征值分解必须要求$A$为方阵，而奇异值分解不需要

3. $A^HA$或$AA^H$的特征值为$A$的奇异值的平方。

4. 我们可以根据对$A^HA$和$AA^H$求特征值和特征向量，从而得到$V$、$U$、$\sum$。