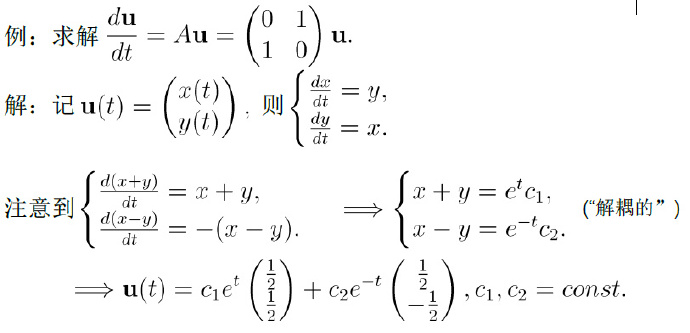本节将矩阵的特征值与微分方程联系在一起，从另一个角度更好地了解特征值。

在差分方程中的应用

首先回顾由差分方程$u_{k+1} = Au]_{k}$描述的离散动力系统的长期行为，即$k\Rightarrow \infty$时解的性质。

设$A$可对角化，即存在可逆矩阵$S=(x_1,...,x_n)$，使得$S^{-1 }A S = \Lambda$为对角阵。

设$S^{-1} u_0 = (c_1,...,c_n)^T$,即$u_0 = c_1x_1 + ... +c_nx_n$。

$u_k = A^ku_0 = S\Lambda ^kS^{-1}u_0 = c_1\lambda_1^kx_1 + ... + c_n\lambda_n^kx_n$

可以看出，$u_k$的增长因子$\lambda_i^k$支配，因此系统的稳定性依赖于$A$的特征值。

当所有特征值$|\lambda_i|<1$时，是稳定的；

当所有特征值$|\lambda_i|\le1$时，是中性稳定的；

当至少有一个特征值$|\lambda_i|>1$时，是不稳定的；

因此，Markov过程是中性稳定的，Fibonacci数列是不稳定的。

引言

设关于t的向量值可导函数$u = u(t) = \begin{pmatrix}u_1(t) \\\\ .... \\\\ u_n(t)\end{pmatrix}$，满足：

$\frac{\mathrm{d} u}{\mathrm{d} x} = Au$

其中$A = (a_{ij})$为$n$阶常数矩阵，求解$u = u(t)$

• 若$A =\begin{pmatrix}\lambda_1 & & \\\\ & ... & \\\\ & & \lambda_n\end{pmatrix}$为对角阵，
  • 则$\frac{\mathrm{d} u_i}{\mathrm{d} x} = \lambda_i u_i$
  • 因此可解得$u = u(t) = \begin{pmatrix}e^{\lambda_1t}c_1\\\\... \\\\ e^{\lambda_nt}c_n\end{pmatrix}$
  • 由于每个方程都是独立的，这类方程被称为解耦的（uncoupled）
• 那么对于一般的矩阵$A$，如何求解呢？
  • 可以将非解耦方程转化为解耦方程求解
  • 

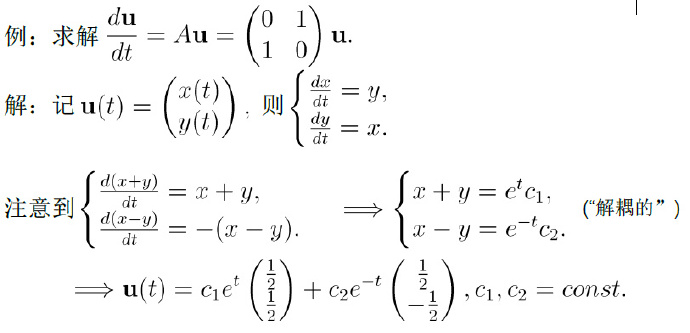
$A$可对角化情形

1. 设$\frac{\mathrm{d} u}{\mathrm{d} t} = Au$有形如$e^{\lambda t}x$的解（为什么要这样假设？），其中$\lambda$为数，$x$为向量，则：

   • $Ax = \lambda x$

   • 因此，$A$的每个特征值$\lambda$及特征向量$x$都会给出$\frac{\mathrm{d} u}{\mathrm{d} t} = Au$的一个解$u = ^{\lambda t}x$。

   • 因此，求解步骤为：

     1. $\frac{\mathrm{d} u}{\mathrm{d} t} = Au = S\Lambda S^{-1}u$
     2. $\frac{\mathrm{d} (S^{-1}u)}{\mathrm{d} t} =\Lambda (S^{-1}u)$
     3. $S^{-1}u = \begin{pmatrix}e^{\lambda_1t}c_1\\\\ ...\\\\ e^{\lambda_nt}c_n\end{pmatrix}$
     4. $u(t) = c_1e^{\lambda_1t}x_1 + ... + c_ne^{\lambda_n t}x_n, u(0) = c_1x_1+...+c_nx_n$

   • 这样，其实我们就使用对角化将非解耦的方程转化为解耦方程，方便求解。

2. 设$u = u_1(t)$和$u = u_2(t)$是齐次线性微分方程组$\frac{\mathrm{d} u}{\mathrm{d} t} = Au$的解，则他们的线性组合$u = c_1u_1(t) + c_2u_2(t)$也是此方程组的解，其中$c_1$和$c_2$是任意常数。

3. $\frac{\mathrm{d} u}{\mathrm{d} t} = A_{n\times n}u$的解集是一个$n$维向量空间。

   • 若$A$可对角化，则方程组的通解为$u(t) = c_1e^{\lambda_1 t}x_1 + ... +c_ne^{\lambda_n t}x_n$

$A$不可对角化时

若$A$不可对角化，设$GM(\lambda ) < AM(\lambda)$。若有相同n个$\lambda$，只有一个特征向量，则这个特征值对应的解为：$c_1e^{\lambda t} x + ....+c_nt^{n-1}e^{\lambda t}x$。

矩阵的指数函数

1. 回顾$e^x = 1+x+\frac{x^2}{2!}+...+\frac{x^n}{n!}+...$

   因此可使用$e^{Ax}$带入，可得：

   $\frac{\mathrm{d} (e^{At})}{\mathrm{d} t} = Ae^{At}$

   而我们需要求的微分方程组$\frac{\mathrm{d} u}{\mathrm{d} t} = Au$，因此$u(t) = e^{At}u(0)$。

2. 矩阵的指数函数性质：

   • 若$\Lambda = \begin{pmatrix}\lambda_1 & & \\\\ & ... & \\\\ & & \lambda_n\end{pmatrix}$, 则$e^{\Lambda t}= \begin{pmatrix}e^{\lambda_1t} & & \\\\& ...& \\\\ & & e^{\lambda_n t}\end{pmatrix}$
   • 若$AB= BA$，则$e^{A+B} = e^A \cdot e^B$，特别的，$(e^A)^{-1} = e^{-A}$。
   • 若存在可逆矩阵$P$,使得$A = PBP^{-1}$，则$e^{At} = P e ^{Bt} P^{-1}$。

3. 因此，若$A$可对角化，由定理一可知：

   $u(t) = e^{At}u(0) = Se^{\Lambda t} S^{-1} u(0) = (x_1,...,x_n)\begin{pmatrix}e^{\lambda_1t} & & \\\\ & ...& \\\\ & & e^{\lambda_n t}\end{pmatrix}\begin{pmatrix}c_1\\\\... \\\\ c_n\end{pmatrix}$

   $= c_1e^{\lambda_1t}x_1 + ... + c_ne^{\lambda_n t}x_n$

$A$二阶常系数线性微分方程

1. 假设$e^{\lambda t}$是方程的解，则可以得特征方程，

   • 若$\lambda_1,\lambda_2$为实数，则方程的通解为：

     $y = c_1 e^{\lambda_1 t} + c_2e^{\lambda_2 t}$

   • 若$\lambda_1,\lambda_2$为共轭负数，即$\lambda_1 = \alpha + i\beta,\lambda_2 = \alpha - i \beta$，则方程的通解为：

     $y = e^{\alpha t}(c_1cos\beta t + c_2 sin\beta t)$

2. 也可以使用矩阵表示为$\frac{\mathrm{d} u}{\mathrm{d} x} = Au$。

3. 若$A$有相同特征值，则不能对角化（为什么？），可使用第一种方法，但要注意，若有$n$重根，则解为$t^0e^{\lambda t},....,t^{n-1}e^{\lambda t}$。

微分方程的稳定性

我们知道若$A$可对角化，则$\frac{\mathrm{d} u}{\mathrm{d} x} = Au$有通解：

$u(t) = c_1e^{\lambda_1t}x_1 + ... + c_ne^{\lambda_n t}x_n$

若所有的实数$\lambda_i < 0$，则解是稳定的；

若所有的实数$\lambda_i \le 0$，则解是中性稳定的；

若至少有一个的实数特征值$\lambda_i < 0$，则解是不稳定的