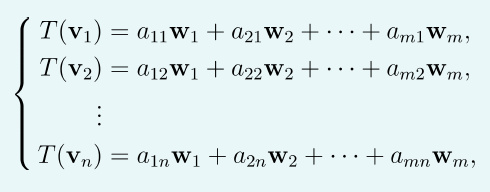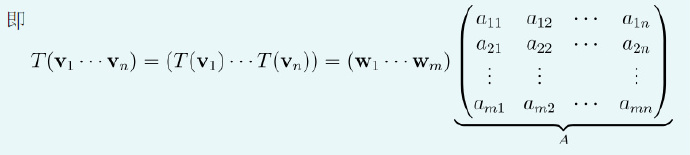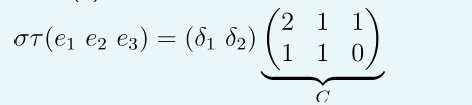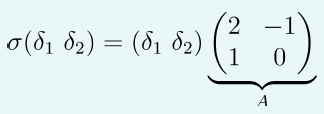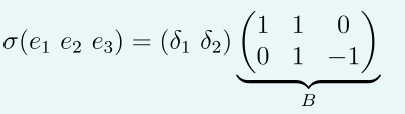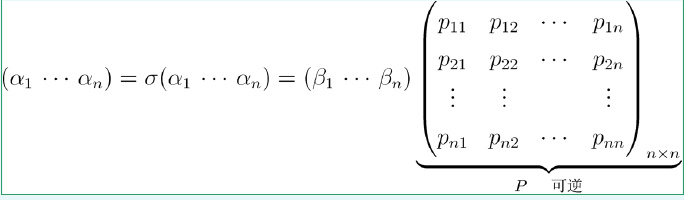每一个矩阵都可以看作是线性变换，矩阵乘法也是由线性变换的复合引出的。

线性变换

理解

线性变换是一种映射，对于向量来说，就是线性空间到线性空间的映射。这里不严格给出线性变换的定义，但举例来说，投影变换、反射变换、不定积分等都可以看做是线性变换。

与线性变换相对的是仿射变换，例如：

$T(x)= Ax + x_0$

就是一个仿射变换，可以通俗的理解为对现象变换$Ax$加上了一个偏移量$x_0$。

性质

由线性变换的性质，我们可以得到：

1. $T(0) = 0,T(-x)= -x$
2. $T(c_1x_1 + c_2 x_2 +...+c_nx_n) = c_1T(x_1)+c_2T(x_2) +...+ c_nT(x_n)$
3. 若$x_1,...,x_n$线性相关，则$T(x_1),...T(x_n)$线性相关。

即线性变换保持向量空间的线性关系。

例如，线性变换总是把直线变成直线，把三角形变成三角形，把平行四边形变成平行四边形。。。

线性变换的矩阵表示

我们想用一个矩阵来表示一个向量中所有线性空间中的变换，也就是用矩阵来描述这个线性变换。

设$V$和$W$分别是数域上$n$维、$m$维向量空间，$T: V \rightarrow W$是$V$到$W$的线性变换。

在$V$中取一组基$v_1,...,v_n$，则对于任意的$v$,可以用基表示为$v = c_1v_1,...,c_nv_n$，这也就是$v$在这组基下的坐标。

因此，$T(v) = c_1T(v_1)+...+c_nT(v_n)$。我们可以发现，要求这个线性空间中任意向量的线性变化，只需要知道基的变换即可。

因此，我们可以在$W$中取一组基$w_1,...,w_m$，则得到基的线性变换为：

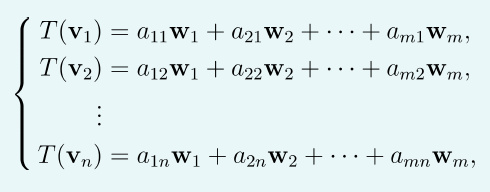
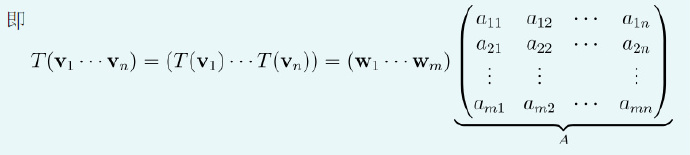
称$m\times n$矩阵$A$为线性变换$T$在$V$中给定基$v_1,....,v_n$和$W$中给定基$w_1,...,w_m$下的矩阵表示。

线性变换与矩阵之间的关系

线性变换的唯一性

对于一个线性变换$\sigma$，在确定了一组基后，对应于唯一的矩阵$A$。

而一个矩阵$A$在一组基下，也对应唯一一个线性变换$\sigma$。

可逆线性变换

设$\sigma \in L(V,V)$为可逆线性变换，且$\sigma$在$V$的某一组基下的矩阵为$A$，则$\sigma^{-1}$在这组基下的矩阵为$A^{-1}$。

例子

设线性变换$t:R^3 \to R^2$定义为$t(x,y,z) = (x+y,y-z)$，线性变换$\sigma:R^2\to R^2$定义为$\sigma(u,v) = (2u-v,u)$，求线性变换$\sigma t:R^3\to R^2$在$R^3$与$R^2$标准基下的矩阵。

注意到：

$\sigma t (x,y,z) = \sigma (t(x,y,z)) = \sigma (x+y,y-z) = (2x+y+z,x+y)$

因此在$R^3$的标准基$e_1,e_2,e_3$与$R^2$的标准基$\delta_1,\delta_2$下有：

$\sigma t (e_1)= \sigma t(1,0,0) = (2,1) = 2\delta_1+\delta _2$

$\sigma t (e_2)= \sigma t(0,1,0) = (1,1) = \delta_1+\delta _2$

$\sigma t (e_3)= \sigma t(0,0,1) = (1,0) = \delta_1$

因此：

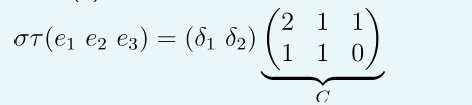
又因为：

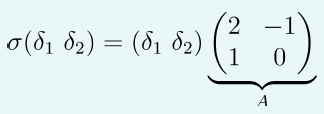
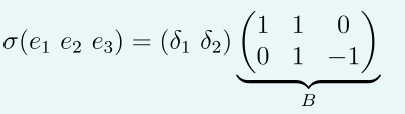
验证可得：

$AB=C$

这就是线性变换的复合。

基变换

我们可以将基变换理解为特殊的线性变换，因为基变换其实是可逆线性变换，也就是说，$A$始终是可逆矩阵。

设$\sigma$是恒同变换，则：

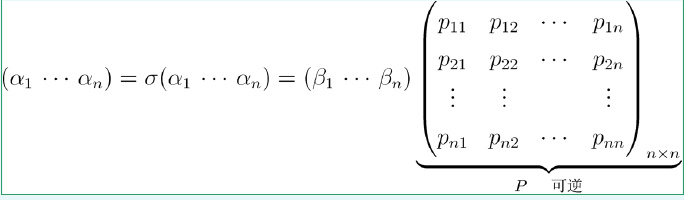
则恒同变换$\sigma$在两组基下的矩阵表示$P$与$V$的这两组基之间的基变换矩阵。

线性变换在不同基下的矩阵

我们发现，线性变换与基的选取有关：同一个线性变换在不同基下的矩阵表示不相同。

因此，我们希望找出线性变换与基无关的性质，或者说，找出线性变换的矩阵表示如何随着基的改变而改变。

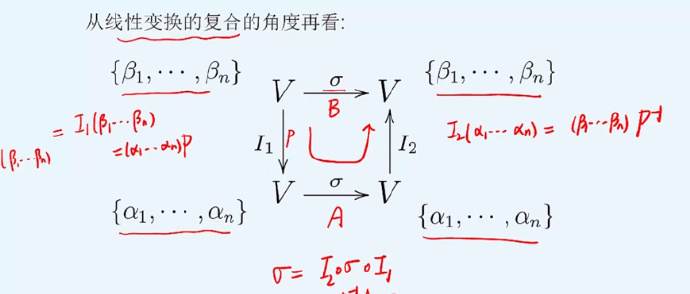
对于这样一个变换，我们既可以通过$B$矩阵直接得到，也可以通过基变换$P$，在新基上用$A$矩阵变换，最后回到原来的基上来表示，因此可以得到：

$B = PAP^{-1}$

我们发现，对于同样一个线性变化，在不同基下的变换矩阵时相似的，同时，可逆矩阵$P$表示这个基变换矩阵。

这是个很好的性质，我们因此可以理解对角化$A = S\Lambda S^{-1}$和奇异值分解$A = U\sum V^T$，在此不再赘述，可以参考目录。

参考资料

1. 线性代数(2)