向量投影是线性代数中很重要的应用，用于找到向量到目标投影空间的投影向量。基本子空间中有着更加特殊和精确的关系，由此可以引出向量空间的正交性及投影等问题。这是下一节线性回归的基础。

$Ax=b$有解时

当计算线性方程组$Ax=b$ 有解时， $b$就在$C(A)$的子空间中，则$Ax= b$在$C(A^T)$中有唯一解。我们考虑$x$的投影。

设$\alpha \in \mathbb {R}^n$是$Ax= b$的解，则$\alpha = \alpha_r + \alpha_n, \alpha_r \in C(A^T), \alpha_n \in N(A)$。则：

$\alpha _r$ 是$\alpha$ 在$C(A^T)$的投影。 $\alpha _n$ 是$\alpha$ 在$N(A)$的投影。

$Ax=b$无解时

当计算线性方程组 $Ax=b$ 时， 它可能是无解的，此时我们可以考虑求 $\hat{x} \in \mathbb{R}^{n}$，使得|| $A \hat{x} - b$ || 最小或极小？

这就意味着当 $b \notin C(A)$ 时，我们需要求解 $C(A)$ 上距离 $b$ 最近的点 $A \hat{x}$ ， 它就是$b$ 在 $C(A)$ 上的投影点。

这对于我们理解最小二乘法很有帮助，具体请参考下一章。

以三维空间为例，目标投影空间可能是线，也可能是面。

投影的实质就是找一个函数，从而使得 $P(B) = b$ ，也就找到了 $B$ 在某一维度的映射。

类似的，在线性代数中，我们需要找到投影矩阵 $P$ ，使得 $Pb \in C(A)$ 。

投影矩阵 $P$

投影矩阵 $P$ ，顾名思义，就是利用矩阵 $P$ ，将向量 $b$ 投影到所需的”空间“中，设投影点为 $p$，则误差向量 $e = b - p$。

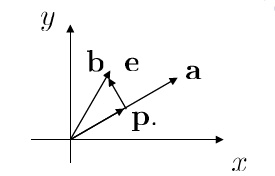
在直线上的投影

求 $b$ 在直线 $a$ 上的投影向量 $p$.

已知 $p + e = b, e \perp a , p = ta (t \in \mathbb{R})$

$\therefore e \perp a \rightarrow a^T(b - ta) = 0 \rightarrow t = \frac{a^Tb}{a^Ta} (a \ne 0)$

即 $b$ 在直线 $a$ 上的投影向量为 $(\frac{a^Tb}{a^Ta} ) a = p$. (a，b表示相应列向量)

投影向量$p = (\frac{a^Tb}{a^Ta} ) a = \frac{a^Ta}{a^Ta} ) b$

我们称 $\frac{a^Ta}{a^Ta}$为投影矩阵 $P$.

在平面上的投影

给定 $v \in \mathbb{R}^3$ ，求 $v$ 在平面 $\pi= C(A)$ 上的投影 $p$ .

令 $\alpha_1, \alpha_2$ 是平面 $\pi$ 上两无关向量，即 $\pi = C(A)$ 的一组基。

令$p = A\hat{x}$，则 $e = v - A\hat{x}$ 垂直于平面 $\pi$ ，即其属于$A$ 的左零空间。

$\therefore A^T(A\hat{X} - v) = 0$， 即 $\hat{x}$ 是 $A^TAx = A^Tv$ 的解。

$\because A$ 的列向量线性无关，即 $A^TA$ 是可逆矩阵

$\therefore \hat{x} = (A^TA)^{-1}A^Tv \rightarrow p = A(A^TA)^{-1}A^Tv$.

我们称 $A(A^TA)^{-1}A^T$ 为投影矩阵 $P$.

一般情形

$A$ 为 $m \times n$ 矩阵，设 $b \in \mathbb{R}^m$，求 $b$ 在 $C(A)$ 上的投影 $p$ ?

$p \in C(A) \Longleftrightarrow \exists \hat{x} \in \mathbb{R}^n, A \hat{x} = p$。

$\because e = b - p \perp C(A) \leftrightarrow e \in N(A^T)$

$\therefore A^T e= \Rightarrow A^T(b - A \hat{x}) = 0. \Longrightarrow p = A\hat{x} = A(A^TA)^{-1}A^Tb$

这里需要注意一点：$A^TAx = A^Tb$ 总有解（无论 $A$ 是否列满秩）

这是因为$C(A^T) = C(A^TA), A^Tb \in C(A^T) = C(A^TA)$，所以总能找到这样的 $\hat{x}$ 使得 $\hat{x} = A(A^TA)^{-1}A^T$。

投影矩阵 $P$的性质

• 若$A$ 的列向量线性无关（列满秩），则矩阵 $A^TA$ 可逆，投影矩阵 $P = A(A^TA)^{-1}A^T$ 满足

$P^2=P, P^T = P$

从直观上，向量 $b$ 经过一次投影到平面$A$ 上后再经过相同的一次投影仍然在平面$A$ 上，因此投影矩阵 $P^2$ 和 $P$ 的效果是一样的，因此$P^2=P$ 。

数学推理：

$P^2 = (A(A^TA)^{-1}A^T)(A(A^TA)^{-1}A^T)) = A(A^TA)^{-1}(A^TA)(A^TA)^{-1}A^T = A(A^TA)^{-1}A^T = P$

• $C(P) = N(I-P), N(P) = C(I-P)$

$\because P^2 = P$

$\therefore P(I-P)=0 \Longrightarrow C(I-P) \subset N(P)$

设 $\alpha \in N(P)$，则 $P\alpha = 0 \Longrightarrow \alpha = (I-P) \alpha$

$\therefore \alpha \in C(I-P) \Longrightarrow N(P) \subset C(I-P)$

综上：$N(P) = C(I-P)$

同理$C(P) = N(I-P)$