向量范数

1. 

2. 对于实向量$x$，下面给出几种常见的范数：

   • 1-范数：

     $||x||_1 = \sum _{i = 1}^n |x_i|$

   • 2-范数：

     $||x||_2 = (\sum _{i = 1}^n |x_i|^2)^{\frac{1}{2}} = (x^Tx)^{\frac{1}{2}}$

   • $\infty$-范数：

     $||x||_{\infty} = max_{1\le i \le n} |x_i|$

3. 由此我们可以定义p-范数为：

   • $||x||_2 = (\sum _{i = 1}^n |x_i|^p)^{\frac{1}{p}},p\ge1$

4. 向量范数的等价性

   • 设$||x||_s$ 和 $||x||_t$为$R^n$上任意两种向量范数，则存在常量$c_1,c_2 > 0$，使得对一切$x \in R^n$有：

   $c_1||x||_s \le ||x||_t \le c_2 ||x||_s$

矩阵范数

1. 

2. 在以上基础上，实际使用的矩阵范数还满足以下相容性条件：

   • $\forall A\in R^{n\times n},x\in R^n ,||Ax|| \le ||A|| \space||x||$

3. 定义矩阵的算子范数为，这衡量了线性变换中对$x$伸缩的最大倍数。

   • $||A||_v = \max\limits_{x\ne 0} \frac {||Ax||_v}{||x||_v}$

   • 我们需要在证明算子范数满足矩阵范数的条件（自己验证）

4. 矩阵$A$的算子范数为:

   • 1-范数：

     • $||A||_1 = \max _{1\le j\le n}\sum_{i=1}^n |a_{ij}|$

   • 2-范数：

     • $||A||_2 = \sqrt{\lambda_{\max}(A^TA)}, \text{表示} A^TA\text{的最大特征值}$

   • $\infty$-范数：

     • $||A||_{\infty} = max_{1\le i \le n} \sum_{j = 1}^n|a_{ij}|$

矩阵条件数

矩阵条件数是衡量非奇异矩阵的敏感程度，也就是方程$Ax = b$中$\Delta A$、$\Delta b$的变化对矩阵的影响程度；我们不加证明的说明一下几个定理。

1. 条件数定义：

   • $cond = \frac{||\Delta x||/||x||}{||\Delta b||/||b||}$

2. 设$A$为非奇异矩阵，则矩阵的条件数为：

   • $cond (A)_v = ||A||_v ||A^{-1}||=\max\limits _{x \ne 0} \frac{||Ax||}{||x||} / \min\limits _{x \ne 0} \frac {||Ax||}{||x||}$

3. 根据条件数的定义，可以推导其和矩阵条件数的关系（考虑方程右边扰动）：

   • $\because A(x +\Delta x) = b + \Delta b$

   • $A \Delta x = \Delta b \Rightarrow \Delta x = A^{-1} \Delta b \Rightarrow ||\Delta x || \le ||A^{-1} ||\space ||\Delta b||$

   • $Ax = b \Rightarrow ||b || \le ||A|| \space ||x||$

   • $\therefore cond = \frac{||\Delta x||/||x||}{||\Delta b||/||b||} = \frac{||\Delta x||\space ||b||}{||\Delta b||\space||x||}\le \frac{||A^{-1}|| \space ||\Delta b|| \space ||A|| \space|| x||}{||\Delta b|| \space ||x||} = ||A|| \space ||A^{-1}||$

4. 矩阵的条件数为误差传递的上限，可衡量矩阵的敏感性

5. 奇异矩阵的条件数为无穷大，因此$cond(A)$越大，越接近于奇异矩阵。

6. 

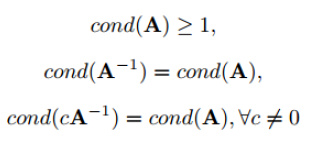
7. 直观的来看，矩阵的条件数反映了矩阵的奇异程度，相对于行列式只能反映是否为奇异矩阵，是一个更好的度量方式。

矩阵的谱半径

1. 设实矩阵$A\in R^{n\times n}$的特征值为$\lambda_i$，称$\rho$为$A$的谱半径：

   • $\rho (A) = \max\limits_{1\le i\le n}|\lambda_i|$

   • 注意，这里的谱半径是指模长（二范数），对于实数来说就是绝对值，对于复数来说是模长。

2. 谱半径的大小不超过任何一种算子范数。

3. 圆盘定理

   • $|\lambda - a_{kk} |\le \sum\limits_{j =1,j \ne k } ^n |a_{kj}|$

   • 直观的来看，在平面中，$A$的每个特征值都属于$A$的格什戈林圆盘中

4. 可以用圆盘定理估计矩阵的特征值范围。

幂法

1. 在矩阵$A$的特征值中，模最大的特征值称为主特征值，也叫“第一特征值”。对应的特征向量为主特征向量。

2. 主特征值可能不唯一（正数负数复数）。

3. 这里注意谱半径和主特征值的区别

   • 谱半径是针对实矩阵而言，计算出来的是特征值的模长（一定大于零）；

   • 主特征值是模长最大的那个特征值（对于复数来说不一样）

4. 如果矩阵有唯一主特征值，则能通过幂法计算出主特征值和特征向量。幂法的计算过程是，首先任取一非零向量$v_0 \in R^n$，再迭代计算

   • $v_k = Av_{k-1}$

   • 根据$v_k$求出主特征值和特征向量。

5. $\lim\limits_{k \rightarrow \infty } \frac {v_k}{\lambda_1 ^k} = x_1$

6. $\lim\limits_{k \rightarrow \infty } \frac {(v_{k+1})_ j}{(v_{k})_j } = \lambda_1$

7. 如果模最大的特征值是重根且非亏损(代数重数等于几何重数)的话幂法适用，但是一旦出现亏损就容易出问题。

8. 幻方矩阵的最大特征值为行和，即为$\frac {n(n^2+1)}{2}$。